题目内容
在正方体ABCD-A1B1C1D1中,AD1与BD所成的角是 .
考点:异面直线及其所成的角
专题:空间角
分析:通过平移直线作出异面直线AD1与BD所成的角,在三角形中即可求得.
解答:
 解:如图,连结BC1、BD和DC1,
解:如图,连结BC1、BD和DC1,
在正方体ABCD-A1B1C1D1中,
由AB=D1C1,AB∥D1C1,可知AD1∥BC1,
所以∠DBC1就是异面直线AD1与BD所成角,
在正方体ABCD-A1B1C1D1中,BC1、BD和DC1是其三个面上的对角线,它们相等.
所以△DBC1是正三角形,∠DBC1=60°
故异面直线AD1与BD所成角的大小为60°.
故答案为60°.
 解:如图,连结BC1、BD和DC1,
解:如图,连结BC1、BD和DC1,在正方体ABCD-A1B1C1D1中,
由AB=D1C1,AB∥D1C1,可知AD1∥BC1,
所以∠DBC1就是异面直线AD1与BD所成角,
在正方体ABCD-A1B1C1D1中,BC1、BD和DC1是其三个面上的对角线,它们相等.
所以△DBC1是正三角形,∠DBC1=60°
故异面直线AD1与BD所成角的大小为60°.
故答案为60°.
点评:本题考查异面直线所成的角及其求法,解决该类题目的基本思路是化空间角为平面角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
数列{an}的通项公式为an=ncos
,其前n项和为Sn,则S2015等于( )
| nπ |
| 2 |
| A、1002 | B、1004 |
| C、1006 | D、-1008 |
若原点和点(1,1)都在直线x+y=a的同一侧,则a的取值范围是( )
| A、a<0或a>2 |
| B、0<a<2 |
| C、a=0或a=2 |
| D、0≤a≤2 |
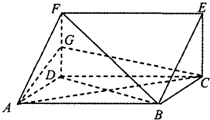 已知三棱柱ADF-BCE中,DF⊥平面ABCD,AD=DC,G是DF的中点
已知三棱柱ADF-BCE中,DF⊥平面ABCD,AD=DC,G是DF的中点