题目内容
如图是函数f(x)=x2+ax+b的部分图象,则函数g(x)=lnx+2x+a的零点所在的区间是( )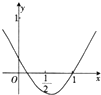

A、(
| ||||
| B、(1,2) | ||||
C、(
| ||||
| D、(2,3) |
考点:二次函数的性质
专题:函数的性质及应用
分析:由二次函数图象的对称轴确定a的范围,据g(x)的表达式计算g(
)和g(1)的值的符号,从而确定零点所在的区间.
| 1 |
| 2 |
解答:
解:由函数f(x)=x2+ax+b的部分图象得0<b<1,f(1)=0,从而-2<a<-1,
而g(x)=lnx+2x+a在定义域内单调递增,
g(
)=ln
+1+a<0,
g(1)=ln1+2+a=2+a>0,
∴函数g(x)=lnx+f′(x)的零点所在的区间是(
,1);
故选C.
而g(x)=lnx+2x+a在定义域内单调递增,
g(
| 1 |
| 2 |
| 1 |
| 2 |
g(1)=ln1+2+a=2+a>0,
∴函数g(x)=lnx+f′(x)的零点所在的区间是(
| 1 |
| 2 |
故选C.
点评:本题主要考查了导数的运算,以及函数零点的判断,同时考查了运算求解能力和识图能力,属于基础题.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
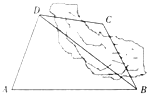 如图,为了计算某湖岸边两景点B与C的距离,由于地形的限制,需要岸上A和D两个测量点,现测得AD⊥CD,AD=10km,AB=14km,∠BDA=60°,∠BCD=135°,则两景点B与C之间的距离为(假设A,B,C,D在同一平面内)( )
如图,为了计算某湖岸边两景点B与C的距离,由于地形的限制,需要岸上A和D两个测量点,现测得AD⊥CD,AD=10km,AB=14km,∠BDA=60°,∠BCD=135°,则两景点B与C之间的距离为(假设A,B,C,D在同一平面内)( )| A、16km | ||
B、8
| ||
C、16
| ||
| D、8km |
已知数列{an}和{bn}满足:a1=1,a2=2,an>0,bn=
,且{bn}是以
为公比的等比数列,若cn=a2n-1+2a2n,则数列{cn}的前n项和为( )
| anan+1 |
| 2 |
| A、5×2n-5 |
| B、3×2n-3 |
| C、2n+1-2 |
| D、2n-1 |
已知数列{an}满足:a1=1,an+1=2an+3(n∈N*),则a9=( )
| A、210-3 |
| B、211-3 |
| C、212-3 |
| D、213-3210-3 |
若0<x<
,则x与2sinx的大小关系为( )
| π |
| 3 |
| A、x>2sinx |
| B、x=2sinx |
| C、x<2sinx |
| D、与x值有关 |