题目内容

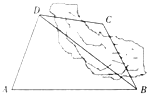如图，为了计算某湖岸边两景点B与C的距离，由于地形的限制，需要岸上A和D两个测量点，现测得AD⊥CD，AD=10km，AB=14km，∠BDA=60°，∠BCD=135°，则两景点B与C之间的距离为（假设A，B，C，D在同一平面内）（　　）
A、16km
B、8
2
km
C、16
2
km
D、8km
考点：解三角形的实际应用
专题：应用题,解三角形
分析：在△ABD中，设BD=x，利用余弦定理求得关于x的方程求得x，进而利用正弦定理求得BC．
解答： 解：在△ABD中，设BD=x，
则BA2=BD2+AD2-2BD•ADcos∠BDA
即142=x2+102-20xcos60°，
整理得x2-10x-96=0，
解之，得x1=16，x2=-6（舍去）
由正弦定理，得
BC
sin∠CDB
=
BD
sin∠BCD
，
所以BC=
16
sin135°
•sin30°=8
2
（km），
故选：B．
点评：本题主要考查了解三角形中的实际应用．以及正弦定理和余弦定理的运用．
练习册系列答案
相关题目
已知△ABC，AC=BC=1，AB=
2
，又已知S是△ABC所在平面外一点，SA=SB=2，SC=
5
，点P是SC的中点，求点P到平面ABC的距离．
在△ABC中，角A，B，C的对边分别为a，b，c，已知c=2
6
，A=45°，a=4，求其它的边和角．
已知双曲线C：
x2
a2
-
y2
b2
=1（a＞0，b＞0），F1，F2为双曲线的左右焦点，若在双曲线的右焦点上存在一点P，使得|PF1|=3|PF2|，则双曲线的离心率的取值范围是
 
．
已知等边△ABC的两个顶点A（0，0），B（4，0），且第三个顶点在第四象限，则BC边所在的直线方程是
 
．
下列函数中，最小值是4的函数的序号是
 

 ①y=x+
4
x
；②y=sinx+
4
sinx
；③y=2ex+2e-x；④y=logx3+4log3x（0＜x＜1）．
已知数列{an}的前n项和为Sn=n2，一△ABC中三边之比为a：b：c=a2：a3：a4，则△ABC的最大内角等于
 
．
光线经过一层玻璃，其强度要损失掉10%，把n块玻璃重叠在一起，通过它的强度减弱到原来的
1
3
以下，则n满足的关系式为（　　）
A、（1-10%）n-1＜
1
3
B、（1-10%）n＜
1
3
C、（1-10%）n+1＜
1
3
D、（1+10%）n＜
1
3
如图是函数f（x）=x2+ax+b的部分图象，则函数g（x）=lnx+2x+a的零点所在的区间是（　　）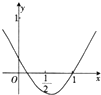
A、（
1
4
，
1
2
）
B、（1，2）
C、（
1
2
，1）
D、（2，3）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网