题目内容
已知f(x)是二次函数,且满足f(0)=1,f(x+1)-f(x)=2x
(1)求f(x)的解析式;
(2)若A={x|x2-4x+3=0},B={x|f(x)=ax}且A∩B=B,求a的取值范围.
(1)求f(x)的解析式;
(2)若A={x|x2-4x+3=0},B={x|f(x)=ax}且A∩B=B,求a的取值范围.
考点:函数解析式的求解及常用方法,交集及其运算
专题:函数的性质及应用
分析:(1)设f(x)=ax2+bx+c,由f(0)=1,f(x+1)-f(x)=2x,求出a,b,c的值即可;
(2)先求出A={1,3},B={x|x2-(a+1)x+1=0},由A∩B=B,只需△≤0,解出a的范围,代入检验即可.
(2)先求出A={1,3},B={x|x2-(a+1)x+1=0},由A∩B=B,只需△≤0,解出a的范围,代入检验即可.
解答:
解:(1)设f(x)=ax2+bx+c
∵f(0)=1,∴c=1
∴f(x+1)-f(x)
=a(x+1)2+b(x+1)+c-ax2-bx-c
=2ax+b+1
=2x
∴2a=2,b+1=0
∴a=1,b=-1,
∴f(x)=x2-x+1;
(2)∵A={x|x2-4x+3=0}={1,3},
B={x|f(x)=ax}={x|x2-(a+1)x+1=0},
∵A∩B=B,
∴对于x2-(a+1)x+1=0,
只需△=(a+1)2-4≤0,
解得:-3≤a≤1,
当a=-3时,B={-1},不合题意,舍,
∴a的取值范围是:(-3,1].
∵f(0)=1,∴c=1
∴f(x+1)-f(x)
=a(x+1)2+b(x+1)+c-ax2-bx-c
=2ax+b+1
=2x
∴2a=2,b+1=0
∴a=1,b=-1,
∴f(x)=x2-x+1;
(2)∵A={x|x2-4x+3=0}={1,3},
B={x|f(x)=ax}={x|x2-(a+1)x+1=0},
∵A∩B=B,
∴对于x2-(a+1)x+1=0,
只需△=(a+1)2-4≤0,
解得:-3≤a≤1,
当a=-3时,B={-1},不合题意,舍,
∴a的取值范围是:(-3,1].
点评:本题考查了求函数的解析式,集合的运算,是一道中档题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
函数f(x)=
在[1,2]的最大值和最小值分别是( )
| 2x |
| x+1 |
A、
| ||||
| B、1,0 | ||||
C、
| ||||
D、1,
|
如图是函数f(x)=x2+ax+b的部分图象,则函数g(x)=lnx+2x+a的零点所在的区间是( )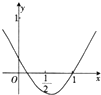

A、(
| ||||
| B、(1,2) | ||||
C、(
| ||||
| D、(2,3) |
两条直线2x-y+k=0和4x-2y+1=0的位置关系是( )
| A、平行 | B、相交 |
| C、重合 | D、平行或重合 |