题目内容
已知数列{an}满足:a1=1,an+1=2an+3(n∈N*),则a9=( )
| A、210-3 |
| B、211-3 |
| C、212-3 |
| D、213-3210-3 |
考点:数列递推式
专题:计算题,等差数列与等比数列
分析:由已知an+1+2an=3,可得an+1+3=-2(an+3),利用等比数列的通项公式即可得出.
解答:
解:由an+1=2an+3,得an+1+3=2(an+3),
∵a1+3=1+3=4≠0,
∴数列{an+3}是以4为首项,以2为公比的等比数列,
∴an+3=2n+1,
∴a9=210-3,
故选:A.
∵a1+3=1+3=4≠0,
∴数列{an+3}是以4为首项,以2为公比的等比数列,
∴an+3=2n+1,
∴a9=210-3,
故选:A.
点评:变形利用等比数列的通项公式是解题的关键.

练习册系列答案
相关题目
如图是函数f(x)=x2+ax+b的部分图象,则函数g(x)=lnx+2x+a的零点所在的区间是( )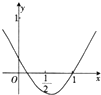

A、(
| ||||
| B、(1,2) | ||||
C、(
| ||||
| D、(2,3) |
两条直线2x-y+k=0和4x-2y+1=0的位置关系是( )
| A、平行 | B、相交 |
| C、重合 | D、平行或重合 |
若函数f(x)满足
>0,则下列关于f(x)的四个判断中正确的是一项是( )
| f′(x) |
| x |
| A、f(x)可能是偶函数 |
| B、f(x)可能是奇函数 |
| C、若-1<x1<x2<1,则f(x1)<f(x2) |
| D、若-1<x1<x2<1,则f(x1)≥f(x2) |
| ∫ |
-
|
| x |
| 2 |
| A、π | B、2 | C、π-2 | D、π+2 |