题目内容

已知数列{an}和{bn}满足：a1=1，a2=2，an＞0，bn=
anan+1
，且{bn}是以
2
为公比的等比数列，若cn=a2n-1+2a2n，则数列{cn}的前n项和为（　　）
A、5×2n-5
B、3×2n-3
C、2n+1-2
D、2n-1
考点：数列递推式
专题：等差数列与等比数列
分析：由已知条件推导出{cn}是等比数列，公比q=2，c1=a1+2a2=5，由此能求出数列{cn}的前n项和．
解答： 解：b1=
a1a2
=
2
，
b2=
2
b1=
a2a3
，a3=
2b12
a2
=2，
bn=b1（
2
）n-1=
anan+1
，
bn+2=b1qn=
an+1an+2
，
anan+1=2（
2
）n-1，
an+2an+1=2（
2
）n+1，
an
an+2
=
1
2
，
an+2=2an，
cn=a2n-1+2a2n，
a2n+2=2a2n，
a2n+1=a2n-1+2=2a2n-1，
cn+1
cn
=
a2n-1+2+2a2n+2
a2n-1+2a2n

=
2(a2n-1+2a2n)
a2n-1+2a2n
=2，
∴{cn}是等比数列，公比q=2，
c1=a1+2a2=5，
∴数列{cn}的前n项和为：
Sn=
5(1-2n)
1-2
=5•2n-5．
故选：A．
点评：本题考查数列的前n项和的求法，是中档题，解题时要认真审题，注意构造法的合理运用．
练习册系列答案
相关题目
在△ABC中，角A，B，C的对边分别为a，b，c，已知c=2
6
，A=45°，a=4，求其它的边和角．
已知数列{an}的前n项和为Sn=n2，一△ABC中三边之比为a：b：c=a2：a3：a4，则△ABC的最大内角等于
 
．
光线经过一层玻璃，其强度要损失掉10%，把n块玻璃重叠在一起，通过它的强度减弱到原来的
1
3
以下，则n满足的关系式为（　　）
A、（1-10%）n-1＜
1
3
B、（1-10%）n＜
1
3
C、（1-10%）n+1＜
1
3
D、（1+10%）n＜
1
3
函数f（x）=
2x
x+1
在[1，2]的最大值和最小值分别是（　　）
A、
4
3
，1
B、1，0
C、
4
3
，
2
3
D、1，
2
3
解关于x的不等式3x2+2x＞2-3x．
定义域在R上的偶函数f（x）在（-∞，0）上是增函数，若f（2a2+a+1）＜f（3a2-2a+1），则实数a的取值范围是
 
．
如图是函数f（x）=x2+ax+b的部分图象，则函数g（x）=lnx+2x+a的零点所在的区间是（　　）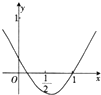
A、（
1
4
，
1
2
）
B、（1，2）
C、（
1
2
，1）
D、（2，3）
∫
π
2
-
π
2
（2cos2
x
2
）dx的值是（　　）
A、πB、2C、π-2D、π+2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网