题目内容
若0<x<
,则x与2sinx的大小关系为( )
| π |
| 3 |
| A、x>2sinx |
| B、x=2sinx |
| C、x<2sinx |
| D、与x值有关 |
考点:不等式比较大小
专题:导数的综合应用
分析:用将不等式问题转化为函数问题,令f(x)=x-2sinx,利用导数法和余弦函数的性质判断函数的单调性,并求出函数值的范围,即可二者的大小关系.
解答:
解:令f(x)=x-2sinx,则f′(x)=1-2cosx,
由0<x<
得,
<cosx<1,则-1<1-2cosx<0,即f′(x)<0,
所以f(x)=x-2sinx在(0,
)单调递减,
则f(x)<f(0)=0-0=0,即f(x)<0成立,
所以x-2sinx<0,即x<2sinx,
故选:C.
由0<x<
| π |
| 3 |
| 1 |
| 2 |
所以f(x)=x-2sinx在(0,
| π |
| 3 |
则f(x)<f(0)=0-0=0,即f(x)<0成立,
所以x-2sinx<0,即x<2sinx,
故选:C.
点评:本题主要考查用函数法来解不等式问题,不等式往往与函数的单调性有关,所以可用单调性或导数来解决.

练习册系列答案
相关题目
光线经过一层玻璃,其强度要损失掉10%,把n块玻璃重叠在一起,通过它的强度减弱到原来的
以下,则n满足的关系式为( )
| 1 |
| 3 |
A、(1-10%)n-1<
| ||
B、(1-10%)n<
| ||
C、(1-10%)n+1<
| ||
D、(1+10%)n<
|
如图是函数f(x)=x2+ax+b的部分图象,则函数g(x)=lnx+2x+a的零点所在的区间是( )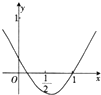

A、(
| ||||
| B、(1,2) | ||||
C、(
| ||||
| D、(2,3) |
若函数f(x)满足
>0,则下列关于f(x)的四个判断中正确的是一项是( )
| f′(x) |
| x |
| A、f(x)可能是偶函数 |
| B、f(x)可能是奇函数 |
| C、若-1<x1<x2<1,则f(x1)<f(x2) |
| D、若-1<x1<x2<1,则f(x1)≥f(x2) |
(文科选作)若等差数列中,a1=2,S3=12,则a6=( )
| A、8 | B、10 | C、12 | D、14 |
| ∫ |
-
|
| x |
| 2 |
| A、π | B、2 | C、π-2 | D、π+2 |