题目内容
数列{an}的首项为3，{bn}为等差数列且bn=an+1-an（n∈N*）．若b3=-2，b10=12，求a8的值．
考点：数列递推式
专题：等差数列与等比数列,点列、递归数列与数学归纳法
分析：本题可以先利用等差数列的通项公式求出数列{bn}的首项和公差，得到该数列的通项，再利用叠加法得到a8的值，即本题答案．
解答：
解：∵{bn}为等差数列，
∴记{bn}的首项为b1，公差为d，
∵b3=-2，b10=12，
∴
∴
，
∴bn=2n-8，n∈N．
∵bn=an+1-an（n∈N*）．
∴a2-a1=b1=-6，
a3-a2=b2=-4，
a4-a3=b3=-2，
…
a8-a7=b7=6．
∴a8-a1=（-6）+（-4）+（-2）+…+6=0．
∵数列{an}的首项为3，
∴a8=3．
∴记{bn}的首项为b1，公差为d，
∵b3=-2，b10=12，
∴
|
∴
|
∴bn=2n-8，n∈N．
∵bn=an+1-an（n∈N*）．
∴a2-a1=b1=-6，
a3-a2=b2=-4，
a4-a3=b3=-2，
…
a8-a7=b7=6．
∴a8-a1=（-6）+（-4）+（-2）+…+6=0．
∵数列{an}的首项为3，
∴a8=3．
点评：本题考查了等差数列的通项公式、递推公式及其应用，本题有一定思维难度，运算量适中，属于中档题．
练习册系列答案
冲刺100分1号卷系列答案
期末好成绩系列答案
相关题目
光线经过一层玻璃，其强度要损失掉10%，把n块玻璃重叠在一起，通过它的强度减弱到原来的
以下，则n满足的关系式为（ ）
| 1 |
| 3 |
A、（1-10%）n-1＜
| ||
B、（1-10%）n＜
| ||
C、（1-10%）n+1＜
| ||
D、（1+10%）n＜
|
若不等式ax2-ax+1≤0解集为空集，则实数a的取值范围是（ ）
| A、（0，4） |
| B、[0，4） |
| C、（0，4] |
| D、[0，4] |
如图是函数f（x）=x2+ax+b的部分图象，则函数g（x）=lnx+2x+a的零点所在的区间是（ ）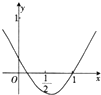
A、（
| ||||
| B、（1，2） | ||||
C、（
| ||||
| D、（2，3） |
若函数f（x）满足
＞0，则下列关于f（x）的四个判断中正确的是一项是（ ）
| f′(x) |
| x |
| A、f（x）可能是偶函数 |
| B、f（x）可能是奇函数 |
| C、若-1＜x1＜x2＜1，则f（x1）＜f（x2） |
| D、若-1＜x1＜x2＜1，则f（x1）≥f（x2） |