题目内容
17.已知一扇形的圆心角是60°,弧长是π,则这个扇形的面积是( )| A. | 3π | B. | $\frac{3π}{2}$ | C. | 6π | D. | $\frac{3π}{4}$ |
分析 根据弧长公式l=$\frac{nπR}{180}$变形,求出半径R,即可求出扇形的面积.
解答 解:∵l=$\frac{nπR}{180}$,
∴R=$\frac{180L}{nπ}$=3,
∴S=$\frac{1}{2}π•3$=$\frac{3π}{2}$,
故选B.
点评 本题考查了扇形的面积,弧长的计算,难度一般,解答本题的关键是能过灵活应用扇形的面积、弧长公式.

练习册系列答案
相关题目
8.log52•log425等于( )
| A. | -1 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
5.已知函数f(x)=alnx的导函数是f′(x)且f′(2)=2,则实数的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | 4 |
12.向量$\overrightarrow{a}$=(2,4,x),$\overrightarrow{b}$=(2,y,2),若|$\overrightarrow{a}$|=6,且$\overrightarrow{a}$⊥$\overrightarrow{b}$,则x+y的值为( )
| A. | -3 | B. | 1 | C. | -3或1 | D. | 3或1 |
6.小明和小东两人比赛下象棋,小明不输的概率是$\frac{3}{4}$,小东输的概率是$\frac{1}{2}$,则两人和棋的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
4.已知|$\overrightarrow{a}$|=3,|$\overrightarrow{b}$|=5,且$\overrightarrow{a}•\overrightarrow{b}$=12,则向量$\overrightarrow{a}$在向量$\overrightarrow{b}$上的投影为( )
| A. | $\frac{12}{5}$ | B. | 4 | C. | $-\frac{12}{5}$ | D. | -4 |
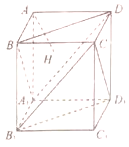 如图,在正方体ABCD-A1B1C1D1中,过点A作平面A1BD的垂线,垂足为点H,给出以下命题:①H是△A1BD的垂心;②AH垂直于平面CB1D1;③AH的延长线过点C1;④直线AH和BB1所成角的大小为45°,其中正确的命题个数为( )
如图,在正方体ABCD-A1B1C1D1中,过点A作平面A1BD的垂线,垂足为点H,给出以下命题:①H是△A1BD的垂心;②AH垂直于平面CB1D1;③AH的延长线过点C1;④直线AH和BB1所成角的大小为45°,其中正确的命题个数为( )