题目内容
6．小明和小东两人比赛下象棋，小明不输的概率是$\frac{3}{4}$，小东输的概率是$\frac{1}{2}$，则两人和棋的概率为（ ）| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{3}{4}$ |
分析 利用互斥事件概率加法公式求解．
解答 解：∵小明和小东两人比赛下象棋，
小明不输的概率是$\frac{3}{4}$，小东输的概率是$\frac{1}{2}$，
∴两人和棋的概率为：p=$\frac{3}{4}-\frac{1}{2}$=$\frac{1}{4}$．
故选：A．
点评 本题考查概率的求法，是基础题，解题时要认真审题，注意互斥事件概率加法公式的合理运用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
17．已知一扇形的圆心角是60°，弧长是π，则这个扇形的面积是（ ）
| A． | 3π | B． | $\frac{3π}{2}$ | C． | 6π | D． | $\frac{3π}{4}$ |
14．函数f（x）=aex-sinx在x=0处有极值，则a的值为（ ）
| A． | -1 | B． | 0 | C． | 1 | D． | e |
11．
利民奶牛场在2016年年初开始改进奶牛饲养方法，同时每月增加一定数目的产奶奶牛，2016年2到5月该奶牛场的产奶量如表所示：
（1）在给定的坐标系中画出表中数据的散点图；
（2）求出y关于x的线性回归方程；
（3）试预测该奶牛场6月份的产奶量？
（注：回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中，$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{x}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$）
利民奶牛场在2016年年初开始改进奶牛饲养方法，同时每月增加一定数目的产奶奶牛，2016年2到5月该奶牛场的产奶量如表所示：| 月份 | 2 | 3 | 4 | 5 |
| 产奶量y（吨） | 2.5 | 3 | 4 | 4.5 |
（2）求出y关于x的线性回归方程；
（3）试预测该奶牛场6月份的产奶量？
（注：回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中，$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{x}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$）
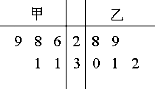为比较甲、乙两地某月14时的气温状况，随机选取该月中的5天，将这5天中14时的气温数据（单位：℃）制成如图所示的茎叶图．考虑以下结论：