题目内容
 已知如图,△ABC是边长为1的正三角形,PA⊥平面ABC,且PA=
已知如图,△ABC是边长为1的正三角形,PA⊥平面ABC,且PA=
| ||
| 4 |
(Ⅰ)求证:PO⊥BC;
(Ⅱ)求线段AA′的长度;
(Ⅲ)求二面角A′-AB-C的余弦值.
考点:二面角的平面角及求法,直线与平面垂直的性质,点、线、面间的距离计算
专题:综合题,空间位置关系与距离,空间角
分析:(Ⅰ)证明PO⊥BC,只需证明BC⊥平面PAE,只需证明BC⊥AO,BC⊥PA;
(Ⅱ)先求AE,再在Rt△PAE中,利用等面积法可求线段AA′的长度;
(Ⅲ)取AB中点为G,连A′G,CG,则∠A′GC即为二面角A'-AB-C的平面角,利用余弦定理求二面角A′-AB-C的余弦值.
(Ⅱ)先求AE,再在Rt△PAE中,利用等面积法可求线段AA′的长度;
(Ⅲ)取AB中点为G,连A′G,CG,则∠A′GC即为二面角A'-AB-C的平面角,利用余弦定理求二面角A′-AB-C的余弦值.
解答:
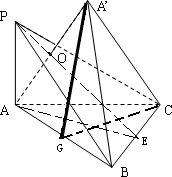 (Ⅰ)证明:由于点A,A'关于平面PBC对称,则连线AA'⊥面PBC,
(Ⅰ)证明:由于点A,A'关于平面PBC对称,则连线AA'⊥面PBC,
所以有BC⊥AO ①
延长PO交BC于E,连结AE,由PA⊥平面ABC知:BC⊥PA ②
由①②知:BC⊥平面PAE且PO?平面PAE,
所以BC⊥PO得证;
(Ⅱ)解:由(Ⅰ)知:BC⊥AE,因为AB=AC=BC=1,
所以E是BC的中点,故可求AE=
,
在Rt△PAE中,利用等面积法可求:AO=
=
=
则AA'=2AO=1;
(Ⅲ)解:根据对称:A′B=A′C=1,从而知A′ABC为正四面体.
取AB中点为G,连A′G,CG,则∠A′GC即为二面角A'-AB-C的平面角
在△A′GC中,A′G=CG=
,A′C=1,
由余弦定理知:cos∠A′GC=
=
故二面角A'-AB-C的余弦值为
.
 (Ⅰ)证明:由于点A,A'关于平面PBC对称,则连线AA'⊥面PBC,
(Ⅰ)证明:由于点A,A'关于平面PBC对称,则连线AA'⊥面PBC,所以有BC⊥AO ①
延长PO交BC于E,连结AE,由PA⊥平面ABC知:BC⊥PA ②
由①②知:BC⊥平面PAE且PO?平面PAE,
所以BC⊥PO得证;
(Ⅱ)解:由(Ⅰ)知:BC⊥AE,因为AB=AC=BC=1,
所以E是BC的中点,故可求AE=
| ||
| 2 |
在Rt△PAE中,利用等面积法可求:AO=
| PA•AE |
| PE |
| ||||||||||
|
| 1 |
| 2 |
则AA'=2AO=1;
(Ⅲ)解:根据对称:A′B=A′C=1,从而知A′ABC为正四面体.
取AB中点为G,连A′G,CG,则∠A′GC即为二面角A'-AB-C的平面角
在△A′GC中,A′G=CG=
| ||
| 2 |
由余弦定理知:cos∠A′GC=
| A′G2+CG2-A′C2 |
| 2A′G•CG |
| 1 |
| 3 |
故二面角A'-AB-C的余弦值为
| 1 |
| 3 |
点评:本题考查知识点较多,综合性强,考查线面垂直的判定与性质的运用,考查面面角,考查学生的计算能力.

练习册系列答案
相关题目
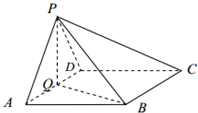 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.