题目内容
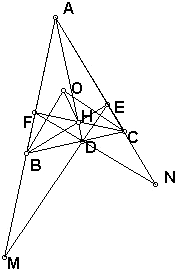 如图,△ABC中,O为外心,三条高AD、BE、CF交于点H,直线ED和AB交于点M,FD和AC交于点N.求证:OB⊥DF.
如图,△ABC中,O为外心,三条高AD、BE、CF交于点H,直线ED和AB交于点M,FD和AC交于点N.求证:OB⊥DF.考点:圆內接多边形的性质与判定
专题:立体几何
分析:由AD、BE、CF分别是△ABC的高,可得A、C、D、F四点共圆,AC为直径,进而由圆内接四边形性质得到∠BDF=∠BAC,由O为△ABC外心,可得∠OBC=
(180°-∠BOC)=90°-∠BAC=90°-∠FDB,进而得到结论.
| 1 |
| 2 |
解答:
解:∵AD、BE、CF分别是△ABC的高,
∴∠AFC=∠ADC=90°,
∴A、C、D、F四点共圆,AC为直径,
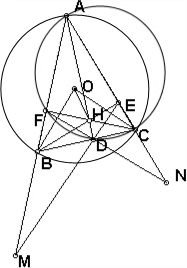
∴∠BDF=∠BAC,
又∠OBC=
(180°-∠BOC)=90°-∠BAC=90°-∠FDB,
即∠OBC+∠FDB=90°,
∴OB⊥DF.
∴∠AFC=∠ADC=90°,
∴A、C、D、F四点共圆,AC为直径,

∴∠BDF=∠BAC,
又∠OBC=
| 1 |
| 2 |
即∠OBC+∠FDB=90°,
∴OB⊥DF.
点评:本题考查的知识点是圆内接四边形的性质与判定,其中分析出A、C、D、F四点共圆,是解答的关键.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
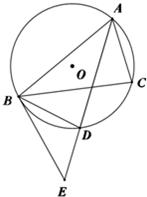 如图,A,B,C是圆O上三个点,AD是∠BAC的平分线,交圆O于D,过B做直线BE交AD延长线于E,使BD平分∠EBC.
如图,A,B,C是圆O上三个点,AD是∠BAC的平分线,交圆O于D,过B做直线BE交AD延长线于E,使BD平分∠EBC.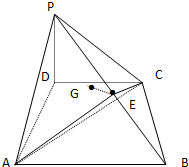 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,∠CDA=∠DAB=90°,PD⊥底面ABCD,PD=AD,CD=1,AB=2,E是PB中点,点E在平面ACP上的射影是△ACP
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,∠CDA=∠DAB=90°,PD⊥底面ABCD,PD=AD,CD=1,AB=2,E是PB中点,点E在平面ACP上的射影是△ACP 如图是一个正方体的表面展开图,A、B、C均为棱的中点,D是顶点,则在正方体中,异面直线AB和CD的夹角的余弦值为
如图是一个正方体的表面展开图,A、B、C均为棱的中点,D是顶点,则在正方体中,异面直线AB和CD的夹角的余弦值为