题目内容
已知函数f（x）=loga（x+1），a＞1，对于定义域内的x1，x2有0＜x1＜x2＜1，给出下列结论：
①（x2-x1）[f（x2）-f（x1）]＜0；
②x2f（x1）＜x1f（x2）；
③f（x2）-f（x1）＞x1-x2；
④
＜f（
）．
其中正确结论的序号是（ ）
①（x2-x1）[f（x2）-f（x1）]＜0；
②x2f（x1）＜x1f（x2）；
③f（x2）-f（x1）＞x1-x2；
④
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
其中正确结论的序号是（ ）
| A、①② | B、①③ | C、②④ | D、③④ |
考点：命题的真假判断与应用,对数函数的图像与性质
专题：函数的性质及应用,简易逻辑
分析：画出函数的图象，可根据函数的单调性判断①的对错；
根据
与
（图象上任意两点与原点连线的斜率）的大小判断②的正误；
再根据函数图象是凸增的，我们可判断③的真假．
根据
| f(x1) |
| x1 |
| f(x2) |
| x2 |
再根据函数图象是凸增的，我们可判断③的真假．
解答：
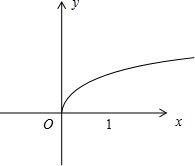解：由已知函数f（x）=loga（x+1），a＞1，函数是增函数，函数的图象如图，
对于定义域内的x1，x2有0＜x1＜x2＜1，
可得x2-x1＞0，f（x2）-f（x1）＞0，
∴（x2-x1）[f（x2）-f（x1）]＞0；显然①不正确；
由x2f（x1）＞x1f（x2）
得
＞
，
即表示两点（x1，f（x1））、（x2，f（x2））与原点连线的斜率的大小，
可以看出结论②正确；
结合函数图象，
由f（x2）-f（x1）＞x2-x1，
可得
＞1，
即两点（x1，f（x1））与（x2，f（x2））连线的斜率大于1，
显然③不正确；
容易判断④的结论是正确的．
故选：C．
解：由已知函数f（x）=loga（x+1），a＞1，函数是增函数，函数的图象如图，对于定义域内的x1，x2有0＜x1＜x2＜1，
可得x2-x1＞0，f（x2）-f（x1）＞0，
∴（x2-x1）[f（x2）-f（x1）]＞0；显然①不正确；
由x2f（x1）＞x1f（x2）
得
| f(x1) |
| x1 |
| f(x2) |
| x2 |
即表示两点（x1，f（x1））、（x2，f（x2））与原点连线的斜率的大小，
可以看出结论②正确；
结合函数图象，
由f（x2）-f（x1）＞x2-x1，
可得
| f(x2)-f(x1) |
| x2-x1 |
即两点（x1，f（x1））与（x2，f（x2））连线的斜率大于1，
显然③不正确；
容易判断④的结论是正确的．
故选：C．
点评：本题考查的知识点是函数的图象和直线的斜率，解答的关键是结合函数图象分析结论中式子的几何意义，然后进行判断．
练习册系列答案
相关题目
“lgx，lgy，lgz成等差数列”是“y2=xz”成立的（ ）
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
i是虚数单位，复数
=（ ）
| 2-3i |
| 1-2i |
A、
| ||
B、
| ||
C、
| ||
D、
|