题目内容
已知球面上有S,A,B,C四点,且SA⊥平面ABC,∠ABC=90°,SC=2.则该球的表面积为 .
考点:球的体积和表面积
专题:计算题,空间位置关系与距离
分析:求得球的直径为SC=2,可得球的半径,即可求出球的表面积.
解答:
解:∵球面上有S,A,B,C四点,且SA⊥平面ABC,∠ABC=90°,SC=2,
∴球的直径为SC=2,
∴球的半径为1,
∴球的表面积为4π.
故答案为:4π.
∴球的直径为SC=2,
∴球的半径为1,
∴球的表面积为4π.
故答案为:4π.
点评:本题考查球的表面积,考查学生的计算能力,比较基础.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
已知函数f(x)=loga(x+1),a>1,对于定义域内的x1,x2有0<x1<x2<1,给出下列结论:
①(x2-x1)[f(x2)-f(x1)]<0;
②x2f(x1)<x1f(x2);
③f(x2)-f(x1)>x1-x2;
④
<f(
).
其中正确结论的序号是( )
①(x2-x1)[f(x2)-f(x1)]<0;
②x2f(x1)<x1f(x2);
③f(x2)-f(x1)>x1-x2;
④
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
其中正确结论的序号是( )
| A、①② | B、①③ | C、②④ | D、③④ |
设a是实数,且
+
(i是虚数单位)是实数,则a=( )
| 1+i |
| i |
| ai |
| 1-i |
| A、2 | ||
B、
| ||
| C、1 | ||
D、
|
在圆x2+y2-2x-6y=0内,过点E(0,1)的最长弦和最短弦分别是AC和BD,则四边形ABCD的面积为( )
A、5
| ||
B、20
| ||
C、15
| ||
D、10
|
 第三赛季甲、乙两名运动员每场比赛得分的茎叶图如图所示,则下列说法中正确的是( )
第三赛季甲、乙两名运动员每场比赛得分的茎叶图如图所示,则下列说法中正确的是( )| A、甲、乙两人单场得分的最高分都是9分 |
| B、甲、乙两人单场得分的中位数相同 |
| C、甲运动员的得分更集中,发挥更稳定 |
| D、乙运动员的得分更集中,发挥更稳定. |
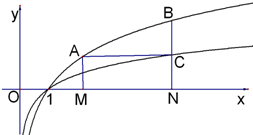 如图,过函数f(x)=logcx(c>1)的图象上的两点A,B作x轴的垂线,垂足分别为M(a,0),N(b,0)(b>a>1),线段BN与函数g(x)=logmx,(m>c>1)的图象交于点C,且AC与x轴平行.
如图,过函数f(x)=logcx(c>1)的图象上的两点A,B作x轴的垂线,垂足分别为M(a,0),N(b,0)(b>a>1),线段BN与函数g(x)=logmx,(m>c>1)的图象交于点C,且AC与x轴平行.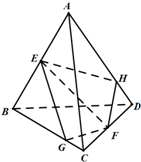 如图,在四面体ABCD中,E,F分别为AB,CD的中点,过EF任作一个平面α分别与直线BC,AD相交于点G,H,有下列三个结论,其中正确的个数是( )
如图,在四面体ABCD中,E,F分别为AB,CD的中点,过EF任作一个平面α分别与直线BC,AD相交于点G,H,有下列三个结论,其中正确的个数是( )