题目内容
函数f（x）=log3（2x2+x）的单调增区间为 ．
考点：复合函数的单调性,对数函数的图像与性质
专题：函数的性质及应用
分析：先求函数的定义域设u（x）=2x2+x则f（x）=lnu（x），因为对数函数的底数3＞1，则对数函数为单调递增函数，要求f（x）函数的增区间只需求二次函数的增区间即可．
解答：
解：由题意可得函数f（x）的定义域是x＞0或x＜-
，
令u（x）=2x2+x的增区间为（0，+∞）
∵3＞1，
∴函数f（x）的单调增区间为（0，+∞）
故答案为：（0，+∞）．
| 1 |
| 2 |
令u（x）=2x2+x的增区间为（0，+∞）
∵3＞1，
∴函数f（x）的单调增区间为（0，+∞）
故答案为：（0，+∞）．
点评：此题考查学生求对数函数及二次函数增减性的能力，以及会求复合函数的增减性的能力．
练习册系列答案
浙江之星课时优化作业系列答案
激活思维优加课堂系列答案
相关题目
设关于x的不等式x2-2x-（a2-2a）＜0的解集为A，若2∈A，则实数a的取值范围为（ ）
| A、（0，2） |
| B、（-∞，0） |
| C、（2，+∞） |
| D、（-∞，0）∪（2，+∞） |
sin(2π-α)cos(
| ||||
tan(α-3π)sin(
|
| A、-cosα | B、cosα |
| C、sinα | D、-sinα |
已知函数f（x）=loga（x+1），a＞1，对于定义域内的x1，x2有0＜x1＜x2＜1，给出下列结论：
①（x2-x1）[f（x2）-f（x1）]＜0；
②x2f（x1）＜x1f（x2）；
③f（x2）-f（x1）＞x1-x2；
④
＜f（
）．
其中正确结论的序号是（ ）
①（x2-x1）[f（x2）-f（x1）]＜0；
②x2f（x1）＜x1f（x2）；
③f（x2）-f（x1）＞x1-x2；
④
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
其中正确结论的序号是（ ）
| A、①② | B、①③ | C、②④ | D、③④ |
在长为5cm的线段AB上任取一点C，以AC，BC为邻边作一矩形，则矩形面积不小于4cm2的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
设a是实数，且
+
（i是虚数单位）是实数，则a=（ ）
| 1+i |
| i |
| ai |
| 1-i |
| A、2 | ||
B、
| ||
| C、1 | ||
D、
|
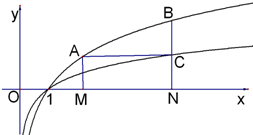如图，过函数f（x）=logcx（c＞1）的图象上的两点A，B作x轴的垂线，垂足分别为M（a，0），N（b，0）（b＞a＞1），线段BN与函数g（x）=logmx，（m＞c＞1）的图象交于点C，且AC与x轴平行．在圆x2+y2-2x-6y=0内，过点E（0，1）的最长弦和最短弦分别是AC和BD，则四边形ABCD的面积为（ ）
A、5
| ||
B、20
| ||
C、15
| ||
D、10
|