题目内容
与120°角终边相同的角的集合是（ ）
| A、{x|x=-600°+k•360°，k∈Z} |
| B、{x|x=-120°+k•360°，k∈Z} |
| C、{x|x=-120°+（2k+1）180°，k∈Z} |
| D、{x|x=-660°+k•360°，k∈Z} |
考点：终边相同的角
专题：计算题
分析：由题目给出的选项可知，在-600°，-120°，660°中只有-600°与120°角终边相同，而选项C可化为{x|x=-300°+k•360°，k∈Z}，300°与120°角终边不相同，由此可得与120°角终边相同的角的集合．
解答：
解：∵120°与-600°终边相同，
∴与120°角终边相同的角的集合是{x|x=-600°+k•360°，k∈Z}．
故选：A．
∴与120°角终边相同的角的集合是{x|x=-600°+k•360°，k∈Z}．
故选：A．
点评：本题考查了终边相同的角，关键是对终边相同角的概念的理解，是基础题．
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
品学双优卷系列答案
相关题目
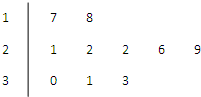如图是某公司10个销售店某月销售某产品数量（单位：台）的茎叶图，则数据落在区间[20，30）内的概率为（ ）| A、0.2 | B、0.4 |
| C、0.5 | D、0.6 |
若a＞0＞b，0＞c＞d则以下不等式中不成立的是（ ）
| A、a+c＞b+d | ||||
| B、a-d＞b-c | ||||
| C、ac＜bd | ||||
D、
|
已知函数f（x）=（x-3）ex，则f′（0）=（ ）
| A、2 | B、-2 | C、3 | D、4 |
| ||
cos20°-
|
A、
| ||
B、
| ||
| C、1 | ||
| D、-1 |
已知函数f（x）=2x+a•2-x（x∈R），则对于任意实数a，函数f（x）不可能是（ ）
| A、奇函数 | B、偶函数 |
| C、单调递增函数 | D、单调递减函数 |
下列四个函数中，既是偶函数又在（0，+∞）上为增函数的是（ ）
| A、f（x）=2x+1 | ||
| B、f（x）=2x2 | ||
C、f（x）=-
| ||
| D、f（x）=-|x| |