题目内容
若a>0>b,0>c>d则以下不等式中不成立的是( )
| A、a+c>b+d | ||||
| B、a-d>b-c | ||||
| C、ac<bd | ||||
D、
|
考点:不等关系与不等式
专题:规律型,不等式的解法及应用
分析:利用同向不等式可相加,判断A正确;
利用在不等式的两边同乘以负数不等号改变,结合同向不等式可相加,判断B正确;
利用同号相乘得正,异号相乘得负,判断C正确;
利用举反例证明D错误.
利用在不等式的两边同乘以负数不等号改变,结合同向不等式可相加,判断B正确;
利用同号相乘得正,异号相乘得负,判断C正确;
利用举反例证明D错误.
解答:
解:∵a>b,c>d,∴a+c>b+d,故A正确;
∵0>c>d,∴-d>-c>0,又a>b,∴a-d>b-c,故B正确;
∵a>0>b,0>c>d,∴ac<0,bd>0,∴ac<bd,故C正确;
若a=1,b=-1,c=-2,d=-4时,
=-
<
=
,故D错误.
故选D.
∵0>c>d,∴-d>-c>0,又a>b,∴a-d>b-c,故B正确;
∵a>0>b,0>c>d,∴ac<0,bd>0,∴ac<bd,故C正确;
若a=1,b=-1,c=-2,d=-4时,
| a |
| d |
| 1 |
| 4 |
| b |
| c |
| 1 |
| 2 |
故选D.
点评:本题考查了不等式的性质,熟练掌握不等式的性质是解答问题的关键.

练习册系列答案
相关题目
一个物体的运动方程为s=-t+t2,其中s的单位是米,t的单位是秒,那么物体在3秒末的瞬时速度是( )
| A、8米/秒 | B、7米/秒 |
| C、6米/秒 | D、5米/秒 |
函数f(x)=
+
的定义域为( )
| 1 |
| x-1 |
| 2+x |
| A、[-2,+∞) |
| B、[-2,1)∪(1,+∞) |
| C、R |
| D、(-∞,-2] |
已知向量
与
的夹角为120°,且|
|=2,|
|=3,若
=λ
+
,且
⊥
,则实数λ的值为( )
| AB |
| AC |
| AB |
| AC |
| AP |
| AB |
| AC |
| AP |
| BC |
A、
| ||
| B、13 | ||
| C、6 | ||
D、
|
函数y=1-2sin2(x-
)是( )
| 3π |
| 4 |
| A、最小正周期为π的奇函数 | ||
| B、最小正周期为π的偶函数 | ||
C、最小正周期为
| ||
D、最小正周期为
|
已知函数f(x)=|log4x|,正实数m、n满足m<n,且f(m)=f(n),若f(x)在区间[m5,n]上的最大值为5,则m、n的值分别为( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
半径为1的圆内接三角形的面积为
,则abc的值为( )
| 1 |
| 4 |
A、
| ||
| B、1 | ||
| C、2 | ||
| D、4 |
与120°角终边相同的角的集合是( )
| A、{x|x=-600°+k•360°,k∈Z} |
| B、{x|x=-120°+k•360°,k∈Z} |
| C、{x|x=-120°+(2k+1)180°,k∈Z} |
| D、{x|x=-660°+k•360°,k∈Z} |
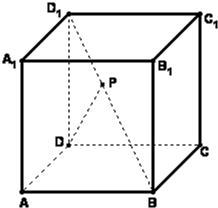 如图,已知正方体ABCD-A1B1C1D1的棱长为a,点P在对角线BD1上,PD与面ABCD所成的角为45°.试建立空间直角坐标系,写出A,B,C,D,A1,B1,C1,D1,P,这9个点的坐标.
如图,已知正方体ABCD-A1B1C1D1的棱长为a,点P在对角线BD1上,PD与面ABCD所成的角为45°.试建立空间直角坐标系,写出A,B,C,D,A1,B1,C1,D1,P,这9个点的坐标.