题目内容
下列四个函数中,既是偶函数又在(0,+∞)上为增函数的是( )
| A、f(x)=2x+1 | ||
| B、f(x)=2x2 | ||
C、f(x)=-
| ||
| D、f(x)=-|x| |
考点:函数单调性的判断与证明,函数奇偶性的判断
专题:函数的性质及应用
分析:根据基本初等函数的单调性奇偶性,逐一分析答案四个函数在(0,+∞)上的单调性和奇偶性,逐一比照后可得答案.
解答:
解:A.f(x)=2x+1在(0,+∞)上单调递增,但为非奇非偶函数;
B.f(x)=2x2在(0,+∞)上单调递增,为偶函数,满足条件;
C.f(x)=-
为奇函数,在(0,+∞)上单调递递增;
D.f(x)=-|x|为偶函数,但在(0,+∞)上单调递减;
故选:B.
B.f(x)=2x2在(0,+∞)上单调递增,为偶函数,满足条件;
C.f(x)=-
| 1 |
| x |
D.f(x)=-|x|为偶函数,但在(0,+∞)上单调递减;
故选:B.
点评:本题考查的知识点是函数的奇偶性与单调性的综合,熟练掌握各种基本初等函数的单调性和奇偶性是解答的关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
已知向量
与
的夹角为120°,且|
|=2,|
|=3,若
=λ
+
,且
⊥
,则实数λ的值为( )
| AB |
| AC |
| AB |
| AC |
| AP |
| AB |
| AC |
| AP |
| BC |
A、
| ||
| B、13 | ||
| C、6 | ||
D、
|
与120°角终边相同的角的集合是( )
| A、{x|x=-600°+k•360°,k∈Z} |
| B、{x|x=-120°+k•360°,k∈Z} |
| C、{x|x=-120°+(2k+1)180°,k∈Z} |
| D、{x|x=-660°+k•360°,k∈Z} |
 执行如图所示的程序框图,输出的S值为64则“ ”处应填( )
执行如图所示的程序框图,输出的S值为64则“ ”处应填( )| A、2 | B、3 | C、4 | D、5 |
某学校高中部组织赴美游学活动,其中高一240人,高二260人,高三300人,现需按年级抽样分配参加名额40人,高二参加人数为( )
| A、12 | B、13 | C、14 | D、15 |
二进制数111111(2)化成十进制数的值是( )
| A、63 | B、62 | C、64 | D、61 |
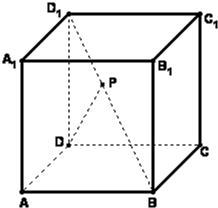 如图,已知正方体ABCD-A1B1C1D1的棱长为a,点P在对角线BD1上,PD与面ABCD所成的角为45°.试建立空间直角坐标系,写出A,B,C,D,A1,B1,C1,D1,P,这9个点的坐标.
如图,已知正方体ABCD-A1B1C1D1的棱长为a,点P在对角线BD1上,PD与面ABCD所成的角为45°.试建立空间直角坐标系,写出A,B,C,D,A1,B1,C1,D1,P,这9个点的坐标.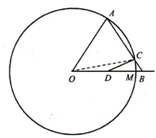 如图,半径为1的圆O上有一定点M,A为圆O上的动点.在射线OM上有一动点B,AB=1,0B>1.线段AB交圆O于另一点C,D为线段的OB中点.求线段CD长的取值范围.
如图,半径为1的圆O上有一定点M,A为圆O上的动点.在射线OM上有一动点B,AB=1,0B>1.线段AB交圆O于另一点C,D为线段的OB中点.求线段CD长的取值范围.