题目内容
已知函数f（x）=2x+a•2-x（x∈R），则对于任意实数a，函数f（x）不可能是（ ）
| A、奇函数 | B、偶函数 |
| C、单调递增函数 | D、单调递减函数 |
考点：函数单调性的判断与证明
专题：函数的性质及应用
分析：分别根据a的取值，结合函数单调性和奇偶性的性质进行判断即可．
解答：
解：若a=0，则f（x）=2x+a•2-x=2x，为单调递增函数，此时C可能．
若a=1，则f（x）=2x+2-x，此时函数为偶函数，B有可能．
若a=-1，则f（x）=2x-2-x，此时函数为奇函数，此时A有可能．
故不可能是D，
故选：D．
若a=1，则f（x）=2x+2-x，此时函数为偶函数，B有可能．
若a=-1，则f（x）=2x-2-x，此时函数为奇函数，此时A有可能．
故不可能是D，
故选：D．
点评：本题主要考查函数奇偶性和单调性的判断，考查学生的推理能力．
练习册系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
函数f(x)=
+
的定义域为（ ）
| 1 |
| x-1 |
| 2+x |
| A、[-2，+∞） |
| B、[-2，1）∪（1，+∞） |
| C、R |
| D、（-∞，-2] |
半径为1的圆内接三角形的面积为
，则abc的值为（ ）
| 1 |
| 4 |
A、
| ||
| B、1 | ||
| C、2 | ||
| D、4 |
与120°角终边相同的角的集合是（ ）
| A、{x|x=-600°+k•360°，k∈Z} |
| B、{x|x=-120°+k•360°，k∈Z} |
| C、{x|x=-120°+（2k+1）180°，k∈Z} |
| D、{x|x=-660°+k•360°，k∈Z} |
（
-
）8 的展开式中的常数项为（ ）
| x |
| 1 | ||
|
| A、56 | B、70 | C、28 | D、60 |
执行如图所示的程序框图，输出的S值为64则“ ”处应填（ ）| A、2 | B、3 | C、4 | D、5 |
某学校高中部组织赴美游学活动，其中高一240人，高二260人，高三300人，现需按年级抽样分配参加名额40人，高二参加人数为（ ）
| A、12 | B、13 | C、14 | D、15 |
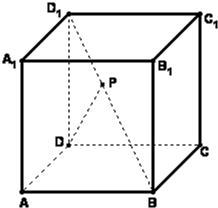如图，已知正方体ABCD-A1B1C1D1的棱长为a，点P在对角线BD1上，PD与面ABCD所成的角为45°．试建立空间直角坐标系，写出A，B，C，D，A1，B1，C1，D1，P，这9个点的坐标．