题目内容
设等差数列{an}的前n项和Sn;且a4-a2=8,S10=190.
(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)求数列{
}的前n项和Tn.
(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)求数列{
| 1 |
| anan+1 |
考点:数列的求和
专题:等差数列与等比数列
分析:(Ⅰ)由已知条件,利用等差数列的通项公式和前n项和公式,列出方程组,求出公差和首项,由此能求出数列{an}的通项公式.
(Ⅱ)根据数列{an}的通项公式,推导出
的表达式,再由裂项求和法能求出数列{
}的前n项和Tn.
(Ⅱ)根据数列{an}的通项公式,推导出
| 1 |
| anan+1 |
| 1 |
| anan+1 |
解答:
解:(Ⅰ)等差数列{an}中,
∵a4-a2=8,S10=190,
∴
,
解得a1=1,d=4,
∴an=1+(n-1)×4=4n-3.
(Ⅱ)∵an=4n-3,
∴
=
=
(
-
),
∴Tn=
(1-
+
-
+…+
-
)
=
(1-
)
=
.
∵a4-a2=8,S10=190,
∴
|
解得a1=1,d=4,
∴an=1+(n-1)×4=4n-3.
(Ⅱ)∵an=4n-3,
∴
| 1 |
| anan+1 |
| 1 |
| (4n-3)(4n+1) |
| 1 |
| 4 |
| 1 |
| 4n-3 |
| 1 |
| 4n+1 |
∴Tn=
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 9 |
| 1 |
| 4n-3 |
| 1 |
| 4n+1 |
=
| 1 |
| 4 |
| 1 |
| 4n+1 |
=
| n |
| 4n+1 |
点评:本题考查数列的通项公式的求法,考查数列的通项公式的求法,解题时要注意裂基求和法的合理运用,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
与120°角终边相同的角的集合是( )
| A、{x|x=-600°+k•360°,k∈Z} |
| B、{x|x=-120°+k•360°,k∈Z} |
| C、{x|x=-120°+(2k+1)180°,k∈Z} |
| D、{x|x=-660°+k•360°,k∈Z} |
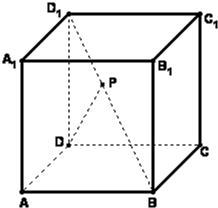 如图,已知正方体ABCD-A1B1C1D1的棱长为a,点P在对角线BD1上,PD与面ABCD所成的角为45°.试建立空间直角坐标系,写出A,B,C,D,A1,B1,C1,D1,P,这9个点的坐标.
如图,已知正方体ABCD-A1B1C1D1的棱长为a,点P在对角线BD1上,PD与面ABCD所成的角为45°.试建立空间直角坐标系,写出A,B,C,D,A1,B1,C1,D1,P,这9个点的坐标.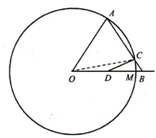 如图,半径为1的圆O上有一定点M,A为圆O上的动点.在射线OM上有一动点B,AB=1,0B>1.线段AB交圆O于另一点C,D为线段的OB中点.求线段CD长的取值范围.
如图,半径为1的圆O上有一定点M,A为圆O上的动点.在射线OM上有一动点B,AB=1,0B>1.线段AB交圆O于另一点C,D为线段的OB中点.求线段CD长的取值范围.