题目内容
设函数f（x）=
的定义域为M，函数g（x）=lg（1+x）的定义域为N，则（ ）
| 1 | ||
|
| A、M∩N=（-1，1] |
| B、M∩N=R |
| C、∁RM=[1，+∞） |
| D、∁RN=（-∞，-1） |
考点：对数函数的定义域
专题：函数的性质及应用
分析：求对数函数的定义域，可得M、N，再利用集合间的运算法则得出结论．
解答：
解：∵函数f（x）=
的定义域为M，函数g（x）=lg（1+x）的定义域为N，
∴M={x|1-x＞0}={x|x＜1}，N={x|1+x＞0}={x|x＞-1}，
∴∁RM=[1，+∞），
故选：C．
| 1 | ||
|
∴M={x|1-x＞0}={x|x＜1}，N={x|1+x＞0}={x|x＞-1}，
∴∁RM=[1，+∞），
故选：C．
点评：本题主要考查求对数函数的定义域，集合间的运算，属于基础题．
练习册系列答案
七星图书口算速算天天练系列答案
初中学业考试导与练系列答案
相关题目
给出下列命题：
（1）实数的共轭复数一定是实数；
（2）满足|z-i|+|z+i|=2的复数z在复平面上对应的点的轨迹是椭圆；
（3）若m∈Z，i2=-1，则im+im+1+im+2+im+3=0；
（4）0＞-i．
其中正确命题的序号是（ ）
（1）实数的共轭复数一定是实数；
（2）满足|z-i|+|z+i|=2的复数z在复平面上对应的点的轨迹是椭圆；
（3）若m∈Z，i2=-1，则im+im+1+im+2+im+3=0；
（4）0＞-i．
其中正确命题的序号是（ ）
| A、（1） |
| B、（1）（3） |
| C、（2）（3） |
| D、（1）（4） |
在复平面内，复数z=
（i为虚数单位）的共轭复数等于（ ）
| 3-i |
| 1+i |
| A、1+2i | B、1-2i |
| C、1+3i | D、-1-3i |
如果直线3x-
y+m=0与双曲线C：
-
=1（a＞0，b＞0）恒有两个公共点，则双曲线C的离心率的取值范围是（ ）
| 3 |
| x2 |
| a2 |
| y2 |
| b2 |
| A、（1，2） |
| B、（2，+∞） |
| C、（1，2] |
| D、[2，+∞） |
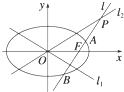已知椭圆C的方程为
如图，已知直线l1：y=4x+m，（m＜0）与抛物线