题目内容
已知抛物线x2=2py(p>0)的焦点为F,顶点为O,准线为l,过该抛物线上异于顶点O的任意一点A作AA1⊥l于点A1,以线段AF,AA1为邻边作平行四边形AFCA1,连接直线AC交l于点D,延长AF交抛物线于另一点B.若△AOB的面积为S△AOB,△ABD的面积为S△ABD,则
的最大值为 .
| (S△AOB)2 |
| S△ABD |
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:由填空题的特殊性,我们可以利用特殊位置进行解决.
解答:
解:由题意,
的最大值,一定在特殊位置取得,即AB⊥x轴,
此时S△AOB=
•
•2p=
p2,
S△ABD=
•p•2p=p2,
∴
的最大值为
=
.
故答案为:
.
| (S△AOB)2 |
| S△ABD |
此时S△AOB=
| 1 |
| 2 |
| p |
| 2 |
| 1 |
| 2 |
S△ABD=
| 1 |
| 2 |
∴
| (S△AOB)2 |
| S△ABD |
| ||
| p2 |
| p2 |
| 4 |
故答案为:
| p2 |
| 4 |
点评:本题考查抛物线的性质,考查三角形面积的计算,考查利用特殊位置解决问题,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知双曲线
-
=1(a>0,b>0)的焦点为F1、F2,渐近线为l1,l2,过点F2且与l1平行的直线交l2于M,若M在以线段F1 F2为直径的圆上,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、2 | ||
B、
| ||
C、
| ||
D、
|
给出下列命题:
(1)实数的共轭复数一定是实数;
(2)满足|z-i|+|z+i|=2的复数z在复平面上对应的点的轨迹是椭圆;
(3)若m∈Z,i2=-1,则im+im+1+im+2+im+3=0;
(4)0>-i.
其中正确命题的序号是( )
(1)实数的共轭复数一定是实数;
(2)满足|z-i|+|z+i|=2的复数z在复平面上对应的点的轨迹是椭圆;
(3)若m∈Z,i2=-1,则im+im+1+im+2+im+3=0;
(4)0>-i.
其中正确命题的序号是( )
| A、(1) |
| B、(1)(3) |
| C、(2)(3) |
| D、(1)(4) |
在复平面内,复数z=
(i为虚数单位)的共轭复数等于( )
| 3-i |
| 1+i |
| A、1+2i | B、1-2i |
| C、1+3i | D、-1-3i |
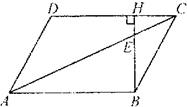 如图,在平行四边形ABCD中,BH⊥CD于点H,BH交AC于点E,已知|
如图,在平行四边形ABCD中,BH⊥CD于点H,BH交AC于点E,已知|