题目内容
 如图所示,一游泳者自游泳池边AB上的D点,沿DC方向游了10米,∠CDB=60°,然后任意选择一个方向并沿此方向继续游,则他再游不超过10米就能够回到游泳池AB边的概率是( )
如图所示,一游泳者自游泳池边AB上的D点,沿DC方向游了10米,∠CDB=60°,然后任意选择一个方向并沿此方向继续游,则他再游不超过10米就能够回到游泳池AB边的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:根据几何概型的概率公式求出对应的测度,即可得到结论.
解答:
解:∵任意选择一个方向,∴对应的度数为360°,
∵再游不超过10米就能够回到游泳池AB边的事件包含的角度为60°,
∴由几何概型的概率公式可得所求的概率P=
=
,
故选:A.
∵再游不超过10米就能够回到游泳池AB边的事件包含的角度为60°,
∴由几何概型的概率公式可得所求的概率P=
| 60 |
| 360 |
| 1 |
| 6 |
故选:A.
点评:本题主要考查几何概型的概率的计算,根据题意求出对应的角度是解决本题的关键,比较基础.

练习册系列答案
相关题目
假设在时间间隔T内的任何时刻,两条不相关的短信机会均等地进入同一台手机.若这两条短信进入手机的间隔时间不大于t(0<t<T)称手机受到干扰,则手机受到干扰的概率是( )
A、(
| ||
B、(1-
| ||
C、1-(
| ||
D、1-(1-
|
下列说法正确的是( )
| A、直角坐标系中横、纵坐标相等的点能够组成一个集合 |
| B、π∈{x|x<3,x∈R} |
| C、∅={0} |
| D、{(1,2)}⊆{1,2,3} |
给出下列命题:
(1)实数的共轭复数一定是实数;
(2)满足|z-i|+|z+i|=2的复数z在复平面上对应的点的轨迹是椭圆;
(3)若m∈Z,i2=-1,则im+im+1+im+2+im+3=0;
(4)0>-i.
其中正确命题的序号是( )
(1)实数的共轭复数一定是实数;
(2)满足|z-i|+|z+i|=2的复数z在复平面上对应的点的轨迹是椭圆;
(3)若m∈Z,i2=-1,则im+im+1+im+2+im+3=0;
(4)0>-i.
其中正确命题的序号是( )
| A、(1) |
| B、(1)(3) |
| C、(2)(3) |
| D、(1)(4) |
如果直线3x-
y+m=0与双曲线C:
-
=1(a>0,b>0)恒有两个公共点,则双曲线C的离心率的取值范围是( )
| 3 |
| x2 |
| a2 |
| y2 |
| b2 |
| A、(1,2) |
| B、(2,+∞) |
| C、(1,2] |
| D、[2,+∞) |
 如图,PA与圆O相切于A,不过圆心O的割线PCB与直径AE相交于D点.已知∠BPA=30°,AD=2,PC=1,则圆O的半径等于
如图,PA与圆O相切于A,不过圆心O的割线PCB与直径AE相交于D点.已知∠BPA=30°,AD=2,PC=1,则圆O的半径等于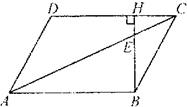 如图,在平行四边形ABCD中,BH⊥CD于点H,BH交AC于点E,已知|
如图,在平行四边形ABCD中,BH⊥CD于点H,BH交AC于点E,已知|