题目内容
一个袋子中装有7个小球,其中红球4个,编号分别为1,2,3,4,黄球3个,编号分别为2,4,6,从袋子中任取4个小球(假设取到任一小球的可能性相等).
(Ⅰ)求取出的小球中有相同编号的概率;
(Ⅱ)记取出的小球的最大编号为X,求随机变量X的分布列和数学期望.
(Ⅰ)求取出的小球中有相同编号的概率;
(Ⅱ)记取出的小球的最大编号为X,求随机变量X的分布列和数学期望.
考点:离散型随机变量的期望与方差,等可能事件的概率
专题:综合题,概率与统计
分析:(Ⅰ)取出的小球中有相同编号,可分成一个相同和两个相同,即可求出概率;
(Ⅱ)随机变量X的可能取值为:3,4,6,求出相应的概率,即可求随机变量X的分布列和数学期望.
(Ⅱ)随机变量X的可能取值为:3,4,6,求出相应的概率,即可求随机变量X的分布列和数学期望.
解答:
解:(Ⅰ)设取出的小球中有相同编号的事件为A,编号相同可分成一个相同和两个相同-------(2分)
P(A)=
=
-----------(4分)
(Ⅱ)随机变量X的可能取值为:3,4,6----------(6分)
P(X=3)=
=
,----------------------(7分)
P(X=4)=
=
,----------------------(8分)
P(X=6)=
=
----------------------(9分)
所以随机变量X的分布列为:
----------------(10分)
所以随机变量X的数学期望EX=3×
+4×
+6×
=
.---------(12分)
P(A)=
2(
| ||||||
|
| 19 |
| 35 |
(Ⅱ)随机变量X的可能取值为:3,4,6----------(6分)
P(X=3)=
| 1 | ||
|
| 1 |
| 35 |
P(X=4)=
| ||||||
|
| 2 |
| 5 |
P(X=6)=
| ||
|
| 4 |
| 7 |
所以随机变量X的分布列为:
| X | 3 | 4 | 6 | ||||||
| P |
|
|
|
所以随机变量X的数学期望EX=3×
| 1 |
| 35 |
| 2 |
| 5 |
| 4 |
| 7 |
| 179 |
| 35 |
点评:本题考查概率的计算,考查随机变量X的分布列和数学期望,考查学生的计算能力,属于中档题.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
下列说法正确的是( )
| A、直角坐标系中横、纵坐标相等的点能够组成一个集合 |
| B、π∈{x|x<3,x∈R} |
| C、∅={0} |
| D、{(1,2)}⊆{1,2,3} |
给出下列命题:
(1)实数的共轭复数一定是实数;
(2)满足|z-i|+|z+i|=2的复数z在复平面上对应的点的轨迹是椭圆;
(3)若m∈Z,i2=-1,则im+im+1+im+2+im+3=0;
(4)0>-i.
其中正确命题的序号是( )
(1)实数的共轭复数一定是实数;
(2)满足|z-i|+|z+i|=2的复数z在复平面上对应的点的轨迹是椭圆;
(3)若m∈Z,i2=-1,则im+im+1+im+2+im+3=0;
(4)0>-i.
其中正确命题的序号是( )
| A、(1) |
| B、(1)(3) |
| C、(2)(3) |
| D、(1)(4) |
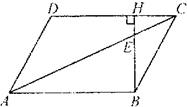 如图,在平行四边形ABCD中,BH⊥CD于点H,BH交AC于点E,已知|
如图,在平行四边形ABCD中,BH⊥CD于点H,BH交AC于点E,已知| 如图,已知直线l1:y=4x+m,(m<0)与抛物线
如图,已知直线l1:y=4x+m,(m<0)与抛物线