题目内容
已知函数
满足①
；②
。
(1)求函数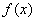
的解析表达式；
（2）若对任意
，都有
成立，求实数
的取值范围。
1）
即
，又
，又
，
。
所以
（2）法一：设
，
则由已知得：
当
即
时，
，此时；
当
即
时，
，解得：无解；
当
即
时，
，此时无解。
综上所述，的取值范围为
。
法二：由已知得，
在上恒成立。由于
在
上单调递增，所以
，故
即。
练习册系列答案
相关题目
题目内容
已知函数满足①；②。
(1)求函数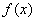的解析表达式；
（2）若对任意，都有成立，求实数的取值范围。
1）即，又，又，。
所以
（2）法一：设，则由已知得：
当即时，，此时；
当即时，，解得：无解；
当即时，，此时无解。
综上所述，的取值范围为。
法二：由已知得，在上恒成立。由于在上单调递增，所以，故即。
＋
＝1(a>b>0)的右焦点为F(3,0)，过点F的直线交椭圆于A、B两点．若AB的中点坐标为(1，－1)，则E的方程为( )
＋
＝1 B.
＋
＝1
＋
＝1 D.
＋
＝1
，若互不相等的实数
满足
，则
的取值范围为（ ）
B. 
C. 
D. 
满足
，设
是方程
的两根，则
的取值范围是 。
＋
＝1的位置关系为( )
＝1的交点为A、B，点P为椭圆上的动点，则使△PAB的面积为
－1的点P的个数为________．
－
＝1(a>0，b>0)的渐近线方程为y＝±
x，若顶点到渐近线的距离为1，则双曲线的方程为( )
－
＝1 B.
－
＝1
＝1
m后，水面的宽度是________m.