题目内容
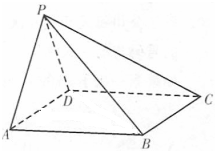四棱锥P-ABCD中，底面ABCD为菱形，且∠DAB=60°，点P为平面ABCD所在平面外的一点，若△PAD为等边三角形，求证：PB⊥AD．考点：棱锥的结构特征
专题：作图题,证明题,空间位置关系与距离
分析：连结BD，取AD的中点E，连结PE，BE；从而可得△ABD也是等边三角形，从而可证AD⊥PE，AD⊥BE，从而证明．
解答：
证明：如图，连结BD，取AD的中点E，连结PE，BE；
从而易知△ABD也是等边三角形，
又∵△PAD为等边三角形，
∴AD⊥PE，AD⊥BE，
又∵PE∩BE=E；
故AD⊥平面PBE；
故AD⊥PB．
证明：如图，连结BD，取AD的中点E，连结PE，BE；从而易知△ABD也是等边三角形，
又∵△PAD为等边三角形，
∴AD⊥PE，AD⊥BE，
又∵PE∩BE=E；
故AD⊥平面PBE；
故AD⊥PB．
点评：本题考查了学生的空间想象力与作图能力，属于基础题．
练习册系列答案
寒假学与练系列答案
相关题目
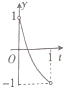
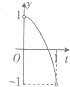
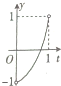
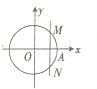在如图所示的直角坐标系中，点A为圆O：x2+y2=1与x轴的交点，垂直于x轴的动直线l从点A出发，以1m/s的速度沿x轴向左移动，记直线l与圆O的交点为M，N，劣弧MN的长为x，令y=cosx，则y与时间t（0＜t＜1，单位：s）的函数y=f（x）的图象大致为（ ）
