题目内容
设函数f(x)=lnx+x2+ax,g(x)=f(x)-x2+1,当a=-1时,证明g(x)≤0在其定义域内恒成立,并证明:
+
+…+
<
,(n∈N,n≥2).
| ln22 |
| 22 |
| ln32 |
| 32 |
| lnn2 |
| n2 |
| 2n2-n-1 |
| 2(n+1) |
考点:利用导数研究函数的单调性
专题:证明题,导数的综合应用,不等式的解法及应用
分析:(1)求出g(x)的导数,求出单调区间,得到极值,判断也为最值,进而证得g(x)≤0在x>0恒成立;
(2)由(1)可得lnx≤x-1,然后转化成n∈N,n≥2,所以lnn2≤n2-1,从而得到
≤
=1-
,再累积加,最后利用裂项求和法得到不等式的右边.
(2)由(1)可得lnx≤x-1,然后转化成n∈N,n≥2,所以lnn2≤n2-1,从而得到
| lnn2 |
| n2 |
| n2-1 |
| n2 |
| 1 |
| n2 |
解答:
证明:(1)由于g(x)=f(x)-x2+1=lnx-x+1,(x>0),g′(x)=
-1,
当x>1时,g′(x)<0,g(x)递减,当0<x<1时,g′(x)>0,g(x)递增,
则g(x)在x=1处取得极大值,也为最大值,且为0,
则g(x)≤0在x>0恒成立;
(2)由(1)得g(x)≤0在(0,+∞)上恒成立.因此lnx≤x-1.
因为n∈N,n≥2,所以lnn2≤n2-1.则
≤
=1-
.
所以
+
+…+
≤(1-
)+(1-
)+…+(1-
)
=(n-1)-(
+
+…+
)
<(n-1)-(
+
+…+
)
=(n-1)-(
-
+
-
+…+
-
)
=(n-1)-(
-
)=
.
所以结论成立.
| 1 |
| x |
当x>1时,g′(x)<0,g(x)递减,当0<x<1时,g′(x)>0,g(x)递增,
则g(x)在x=1处取得极大值,也为最大值,且为0,
则g(x)≤0在x>0恒成立;
(2)由(1)得g(x)≤0在(0,+∞)上恒成立.因此lnx≤x-1.
因为n∈N,n≥2,所以lnn2≤n2-1.则
| lnn2 |
| n2 |
| n2-1 |
| n2 |
| 1 |
| n2 |
所以
| ln22 |
| 22 |
| ln32 |
| 32 |
| lnn2 |
| n2 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| n2 |
=(n-1)-(
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| n2 |
<(n-1)-(
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| n(n+1) |
=(n-1)-(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
=(n-1)-(
| 1 |
| 2 |
| 1 |
| n+1 |
| 2n2-n-1 |
| 2(n+1) |
所以结论成立.
点评:本题主要考查了了利用导数研究函数的极值,以及利用导数研究函数的单调性和不等式的证明,属于难题.

练习册系列答案
相关题目
已知直线l1:x-2y+1=0与l2:2x+ky+3=0平行,则k的值是( )
A、
| ||
B、-
| ||
| C、-4 | ||
| D、4 |
集合A={x|-2≤x≤2},B={y|y=
,0≤x≤4},则下列关系正确的是( )
| x |
| A、A⊆∁RB |
| B、B⊆∁RA |
| C、∁RA⊆∁RB |
| D、A∪B=R |
在长为6cm的线段AB上任取一点C,现作一矩形,邻边长分别等于线段AC,BC的长,则该矩形面积小于8cm2,的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 在锐角△ABC中,BC=5,sinA=
在锐角△ABC中,BC=5,sinA=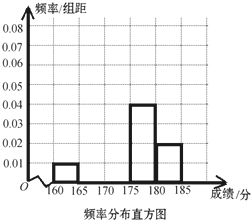 永安市教育局在2013年高职单招考试成绩中随机抽取100名学生的成绩,按成绩分组,得到频率分布表如下所示:
永安市教育局在2013年高职单招考试成绩中随机抽取100名学生的成绩,按成绩分组,得到频率分布表如下所示: