题目内容
△ABC中，a、b、c分别是角A、B、C的对边，已知b2+c2=a2+bc，
•
=4，求S△ABC．
| AC |
| AB |
考点：余弦定理,正弦定理
专题：解三角形
分析：由条件里哦也难怪余弦定理求得cosA=
的值，可得A的值．根据
•
=4，求得AB•AC=8，再根据 S△ABC =
•AB•AC•sinA，计算求得结果．
| b2+c2-a2 |
| 2bc |
| AC |
| AB |
| 1 |
| 2 |
解答：
解：△ABC中，∵b2+c2=a2+bc，
∴cosA=
=
，∴A=
．
又
•
=AB•AC•cosA=AB•AC•
=4，∴AB•AC=8
∴S△ABC =
•AB•AC•sinA=
×8×
=2
．
∴cosA=
| b2+c2-a2 |
| 2bc |
| 1 |
| 2 |
| π |
| 3 |
又
| AC |
| AB |
| 1 |
| 2 |
∴S△ABC =
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
点评：本题主要考查余弦定理、两个向量的数量积的定义，属于中档题．
练习册系列答案
相关题目
已知数列{an}首项为1，且满足an+1=
an，那么an等于（ ）
| n+1 |
| n |
| A、n | ||
| B、n+1 | ||
C、
| ||
D、
|
若数列{an}的前n项和Sn=3n2-10n，则数列的前10项中正数项的和为（ ）
| A、106 | B、208 |
| C、216 | D、118 |
要做一个圆锥形的漏斗，其母线长为40cm，要使其体积为最大，则高为（ ）
A、
| ||||
B、
| ||||
C、10
| ||||
D、
|
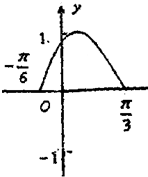已知函数f（x）=sin（ωx+φ）（其中ω＞0，|φ|＜
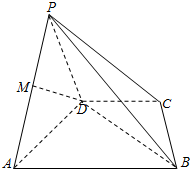如图，四棱锥P-ABCD中，底面ABCD是直角梯形，AB∥CD，∠DAB=60°，AB=AD=2CD，侧面PAD⊥底面ABCD，且△PAD为等腰直角三角形，∠APD=90°，M为AP的中点．