题目内容
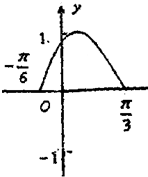已知函数f（x）=sin（ωx+φ）（其中ω＞0，|φ|＜| π |
| 2 |
| π |
| 6 |
| π |
| 3 |
（1）求ω，φ的值；
（2）设x∈[0，
| 5π |
| 12 |
考点：由y=Asin（ωx+φ）的部分图象确定其解析式,正弦函数的图象
专题：三角函数的图像与性质
分析：（1）直接由图象求得周期，再由周期公式求得ω，然后结合五点作图的第一点求φ；
（2）把（1）中求得的f（x）代入|4f（x）-1|，结合x的范围求得|4f（x）-1|的范围，则满足|4f（x）-1|＜m恒成立的实数m的取值范围可求．
（2）把（1）中求得的f（x）代入|4f（x）-1|，结合x的范围求得|4f（x）-1|的范围，则满足|4f（x）-1|＜m恒成立的实数m的取值范围可求．
解答：
解：（1）由图象可知，
=
-(-
)=
，
∴T=
=π，则ω=2．
由五点作图的第一点可知，2×(-
)+φ=0，得φ=
；
（2）由（1）得f（x）=sin（2x+
），
代入|4f（x）-1|＜m，得|4sin（2x+
）-1|＜m．
∵x∈[0，
]，
∴2x+
∈[
，
]，
∴4sin（2x+
）-1∈[-3，3]．
则|4sin（2x+
）-1|∈[0，3]．
∴m＞3．
故实数m的取值范围是（3，+∞）．
| T |
| 2 |
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
∴T=
| 2π |
| ω |
由五点作图的第一点可知，2×(-
| π |
| 6 |
| π |
| 3 |
（2）由（1）得f（x）=sin（2x+
| π |
| 3 |
代入|4f（x）-1|＜m，得|4sin（2x+
| π |
| 3 |
∵x∈[0，
| 5π |
| 12 |
∴2x+
| π |
| 3 |
| π |
| 3 |
| 7π |
| 6 |
∴4sin（2x+
| π |
| 3 |
则|4sin（2x+
| π |
| 3 |
∴m＞3．
故实数m的取值范围是（3，+∞）．
点评：本题考查了由函数y=Asin（ωx+φ）的部分图象求函数解析式，考查了三角函数值域的求法，是中档题．
练习册系列答案
核心素养学练评系列答案
单元期中期末卷系列答案
相关题目
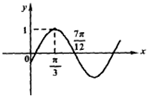已知导函数f′（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜| π |
| 2 |
| ||
| 4 |
| 1 |
| 2 |
A、先把各点的横坐标缩短到原来的
| ||||
B、先把各点的横坐标伸长到原来的2倍，再向右平移
| ||||
C、先把各点的横坐标缩短到原来的
| ||||
D、先把各点的横坐标伸长到原来的2倍，再向左平移
|
在数学归纳法证明“1+a+a2+…+an=
（a≠1，n∈N*）”时，验证当n=1时，等式的左边为（ ）
| 1-an+1 |
| 1-a |
| A、1 |
| B、1-a |
| C、1+a |
| D、1-a2 |
数列2，5，8，11，…，则23是这个数列的（ ）
| A、第5项 | B、第6项 |
| C、第7项 | D、第8项 |
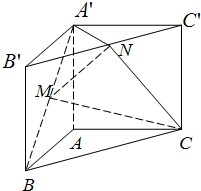如图，直三棱柱ABC-A′B′C′，∠BAC=90°，AB=AC=