题目内容
若数列{an}的前n项和Sn=3n2-10n,则数列的前10项中正数项的和为( )
| A、106 | B、208 |
| C、216 | D、118 |
考点:等差数列的前n项和
专题:等差数列与等比数列
分析:由已知条件推导出an=6n-13,由此能求出数列的前10项中正数项的和.
解答:
解:∵数列{an}的前n项和Sn=3n2-10n,
∴a1=S1=3-10=-7,
当n≥2时,Sn-Sn-1=(3n2-10n)-[3(n-1)2-10(n-1)]
=6n-13,
当n=1时,6n-13=-7=a1,
∴an=6n-13,a1=6-13=-7,a2=6×2-13=-1,
d=a2-a1=6,
由an=6n-13≥0,得n≥
,
∵a2<0,a3>0,
∴数列的前10项中正数项的和:
S=S10-S2=(10a1+
d)-(a1+a2)
=10×(-7)+
×6-(-7-1)
=208.
故选:B.
∴a1=S1=3-10=-7,
当n≥2时,Sn-Sn-1=(3n2-10n)-[3(n-1)2-10(n-1)]
=6n-13,
当n=1时,6n-13=-7=a1,
∴an=6n-13,a1=6-13=-7,a2=6×2-13=-1,
d=a2-a1=6,
由an=6n-13≥0,得n≥
| 13 |
| 6 |
∵a2<0,a3>0,
∴数列的前10项中正数项的和:
S=S10-S2=(10a1+
| 10×9 |
| 2 |
=10×(-7)+
| 10×9 |
| 2 |
=208.
故选:B.
点评:本题考查数列的前10项中正数和的求法,是中档题,解题时要认真审题,注意等差数列的性质的灵活运用.

练习册系列答案
相关题目
根据如图的流程图,则输出的结果是( )


| A、7 | B、8 | C、720 | D、5040 |
在一次独立性检验中,得出2×2列联表如下:K2=
且最后发现,两个分类变量A和B没有任何关系,则a的可能值是( )
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| A |
|
合计 | |||
| B | 200 | 800 | 1000 | ||
|
180 | a | 180+a | ||
| 合计 | 380 | 800+a | 1180+a |
| A、200 | B、720 |
| C、100 | D、180 |
在数学归纳法证明“1+a+a2+…+an=
(a≠1,n∈N*)”时,验证当n=1时,等式的左边为( )
| 1-an+1 |
| 1-a |
| A、1 |
| B、1-a |
| C、1+a |
| D、1-a2 |
方程a2•sin2x+asinx-2=0有解的条件是( )
| A、|a|≤1 | B、|a|≥1 |
| C、|a|≥2 | D、a∈R |
数列2,5,8,11,…,则23是这个数列的( )
| A、第5项 | B、第6项 |
| C、第7项 | D、第8项 |
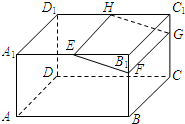 如图,在长方体ABCD-A1B1C1D1中,E,H分别是棱A1B1,D1C1上的点(点E与B1不重合),且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G.设AB=2AA1=2a.在长方体ABCD-A1B1C1D1内随机选取一点,记该点取自于几何体A1ABFE-D1DCGH内的概率为P,当点E,F分别在棱A1B1,BB1上运动且满足EF=a时,则P的最小值为( )
如图,在长方体ABCD-A1B1C1D1中,E,H分别是棱A1B1,D1C1上的点(点E与B1不重合),且EH∥A1D1,过EH的平面与棱BB1,CC1相交,交点分别为F,G.设AB=2AA1=2a.在长方体ABCD-A1B1C1D1内随机选取一点,记该点取自于几何体A1ABFE-D1DCGH内的概率为P,当点E,F分别在棱A1B1,BB1上运动且满足EF=a时,则P的最小值为( )