题目内容
要做一个圆锥形的漏斗,其母线长为40cm,要使其体积为最大,则高为( )
A、
| ||||
B、
| ||||
C、10
| ||||
D、
|
考点:导数在最大值、最小值问题中的应用,旋转体(圆柱、圆锥、圆台)
专题:导数的综合应用,空间位置关系与距离
分析:设出圆锥的高,求出底面半径,推出体积的表达式,利用导数求出体积的最大值时的高即可.
解答:
解:设圆锥的高为h cm,
∴V圆锥=
π(1600-h2)×h,
∴V′(h)=π(1600-3h2).令V′(h)=0,
得h2=
,∴h=
(cm)
当0<h<
时,V′>0;
当
<h<20时,V′<0,
∴当h=
时,V取最大值.
故选:D.
∴V圆锥=
| 1 |
| 3 |
∴V′(h)=π(1600-3h2).令V′(h)=0,
得h2=
| 1600 |
| 3 |
40
| ||
| 3 |
当0<h<
40
| ||
| 3 |
当
40
| ||
| 3 |
∴当h=
40
| ||
| 3 |
故选:D.
点评:本题考查旋转体问题,以及利用导数求函数的最值问题,考查计算能力,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列选项中,p是q的必要不充分条件的是( )
A、p:f(x)=x3+2x2+mx+1在R上单调递增;q:m≥
| ||
| B、p:x=1;q:x=x2 | ||
| C、p:a+bi(a,b∈R)是纯虚数;q:a=0 | ||
| D、p:a+c>b+d;q:a>b且c>d |
在一次独立性检验中,得出2×2列联表如下:K2=
且最后发现,两个分类变量A和B没有任何关系,则a的可能值是( )
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| A |
|
合计 | |||
| B | 200 | 800 | 1000 | ||
|
180 | a | 180+a | ||
| 合计 | 380 | 800+a | 1180+a |
| A、200 | B、720 |
| C、100 | D、180 |
方程a2•sin2x+asinx-2=0有解的条件是( )
| A、|a|≤1 | B、|a|≥1 |
| C、|a|≥2 | D、a∈R |
数列2,5,8,11,…,则23是这个数列的( )
| A、第5项 | B、第6项 |
| C、第7项 | D、第8项 |
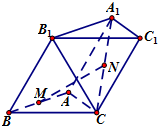 如图,已知三棱柱ABC-A1B1C1,侧面BCC1B1⊥底面ABC.
如图,已知三棱柱ABC-A1B1C1,侧面BCC1B1⊥底面ABC.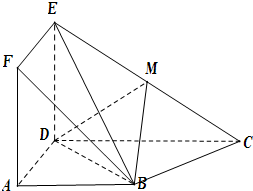 如图,正方形ADEF与梯形ABCD所在平面互相垂直,AD⊥CD,AB∥CD,AB=AD=
如图,正方形ADEF与梯形ABCD所在平面互相垂直,AD⊥CD,AB∥CD,AB=AD=