题目内容
 将边长为4的正方形ABCD和等腰直角三角形ABE按图拼为新的几何图形,△ABE中,AB=AE,连结DE,CE,若DE=4
将边长为4的正方形ABCD和等腰直角三角形ABE按图拼为新的几何图形,△ABE中,AB=AE,连结DE,CE,若DE=4| 2 |
(Ⅰ)求CM与DE所成角的大小;
(Ⅱ)若N为CE中点,证明:MN∥平面ADE;
(Ⅲ)证明:平面CAM⊥平面CBE.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:(Ⅰ)分别以AE,AB,AD所在直线为x,y,z轴,建立空间直角坐标系,利用向量法能求出CM与DE所成角.
(Ⅱ)利用向量法推导出
与
共线,由此能证明MN∥平面ADE.
(Ⅲ)由已知条件推导出AM⊥BC,AM⊥BE,由此能证明平面CAM⊥平面CBE.
(Ⅱ)利用向量法推导出
| MN |
| AD |
(Ⅲ)由已知条件推导出AM⊥BC,AM⊥BE,由此能证明平面CAM⊥平面CBE.
解答:
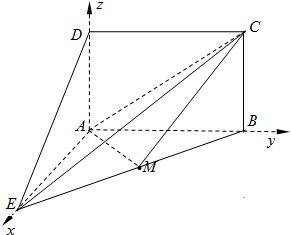 (Ⅰ)解:∵AE=AD=4,DE=4
(Ⅰ)解:∵AE=AD=4,DE=4
,
∴DA⊥AE,又DA⊥AB,AB∩AE=A
∴DA⊥面BAE,△ABE为等腰直角三角形,且AB=AE,
∴∠BAE=90°,AE,AB,AD两两垂直,
分别以AE,AB,AD所在直线为x,y,z轴,
建立空间直角坐标系如图:
则E(4,0,0),D(0,0,4),
=(4,0,-4),
M(2,2,0),C(0,4,4)
∴
=(2,-2,-4)
∴cos<
,
>=
=
=
∴CM与DE所成角的大小为
…(4分)
(Ⅱ)解:∵E(4,0,0),C(0,4,4),N为CE中点
∴N(2,2,2),而M(2,2,0)
∴
=(2,2,2)-(2,2,0)=(0,0,2)
=(0,0,4)
∴
与
共线,MN∥AD,AD?面ADE,MN?面ADE,
∴MN∥平面ADE…(8分)
(Ⅲ)证明:DA⊥面BAE,AM?面BAE,
∴DA⊥AM,BC∥DA,
∴AM⊥BC,
又△ABE为等腰直角三角形且M为斜边BE中点,
∴AM⊥BE,BE∩BC=B,
∴AM⊥面BCE,
又AM?面CAM,
∴平面CAM⊥平面CBE.…(12分)
 (Ⅰ)解:∵AE=AD=4,DE=4
(Ⅰ)解:∵AE=AD=4,DE=4| 2 |
∴DA⊥AE,又DA⊥AB,AB∩AE=A
∴DA⊥面BAE,△ABE为等腰直角三角形,且AB=AE,
∴∠BAE=90°,AE,AB,AD两两垂直,
分别以AE,AB,AD所在直线为x,y,z轴,
建立空间直角坐标系如图:
则E(4,0,0),D(0,0,4),
| DE |
M(2,2,0),C(0,4,4)
∴
| CM |
∴cos<
| CM |
| DE |
| ||||
|
|
| (2,-2,-4)•(4,0,-4) | ||||
|
| ||
| 2 |
∴CM与DE所成角的大小为
| π |
| 6 |
(Ⅱ)解:∵E(4,0,0),C(0,4,4),N为CE中点
∴N(2,2,2),而M(2,2,0)
∴
| MN |
| AD |
∴
| MN |
| AD |
∴MN∥平面ADE…(8分)
(Ⅲ)证明:DA⊥面BAE,AM?面BAE,
∴DA⊥AM,BC∥DA,
∴AM⊥BC,
又△ABE为等腰直角三角形且M为斜边BE中点,
∴AM⊥BE,BE∩BC=B,
∴AM⊥面BCE,
又AM?面CAM,
∴平面CAM⊥平面CBE.…(12分)
点评:本题考查异面直线所成角的大小的求法,考查直线与平面平行的证明,考查平面与平面垂直的证明,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
过点P(3,2),且在两坐标轴上的截距相等的直线方程为( )
| A、2x-3y=0 |
| B、x+y-6=0 |
| C、x+y-5=0 |
| D、2x-3y=0或x+y-5=0 |
 如图,矩形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=DE=1,CD=2,M为CE上的点.
如图,矩形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=DE=1,CD=2,M为CE上的点. 如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AD=1,点M是SD的中点,AN⊥SC,交SC于点N.
如图,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥底面ABCD,SA=AD=1,点M是SD的中点,AN⊥SC,交SC于点N. 如图所示,已知AC⊥平面CDE,BD∥AC,△ECD为等边三角形,F为ED边上的中点,且CD=BD=2AC=2,
如图所示,已知AC⊥平面CDE,BD∥AC,△ECD为等边三角形,F为ED边上的中点,且CD=BD=2AC=2,