题目内容
 如图所示,已知AC⊥平面CDE,BD∥AC,△ECD为等边三角形,F为ED边上的中点,且CD=BD=2AC=2,
如图所示,已知AC⊥平面CDE,BD∥AC,△ECD为等边三角形,F为ED边上的中点,且CD=BD=2AC=2,(1)求证:CF∥面ABE;
(2)求证:面ABE⊥平面BDE;
(3)求该几何体ABECD的体积.
考点:平面与平面垂直的判定,组合几何体的面积、体积问题
专题:空间位置关系与距离
分析:(1)取BE的中点G,连结FG,推导出CF∥AG,由此能证明CF∥面ABE.
(2)由△ECD为等边三角形,推导出AG⊥面BDE,由此能证明面ABE⊥平面BDE.
(3)几何体ABECD是四棱锥E-ABCD,由此能求出该几何体ABECD的体积.
(2)由△ECD为等边三角形,推导出AG⊥面BDE,由此能证明面ABE⊥平面BDE.
(3)几何体ABECD是四棱锥E-ABCD,由此能求出该几何体ABECD的体积.
解答:
解:(1)取BE的中点G,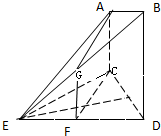
连FG,∵FG∥
BD,AC∥
BD,
∴CF∥AG,
又CF不包含于面ABE,AG?面ABE,
∴CF∥面ABE,…(4分)
(2)∵△ECD为等边三角形,
∴CF⊥ED又CF⊥BD,
∴CF⊥面BDE,CF∥AG
∴AG⊥面BDE,
又AG?平面ABE,∴面ABE⊥平面BDE,…(8分)
(3)几何体ABECD是四棱锥E-ABCD,EH⊥CD
∴EH⊥面ABCD,
∴VE-ABCD=
•
(1+2)•2•
=
.…(12分)

连FG,∵FG∥
| 1 |
| 2 |
| 1 |
| 2 |
∴CF∥AG,
又CF不包含于面ABE,AG?面ABE,
∴CF∥面ABE,…(4分)
(2)∵△ECD为等边三角形,
∴CF⊥ED又CF⊥BD,
∴CF⊥面BDE,CF∥AG
∴AG⊥面BDE,
又AG?平面ABE,∴面ABE⊥平面BDE,…(8分)
(3)几何体ABECD是四棱锥E-ABCD,EH⊥CD
∴EH⊥面ABCD,
∴VE-ABCD=
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
点评:本题考查直线与平面平行的证明,考查平面与平面垂直的证明,考查几何体体积的求法,解题时要注意空间思维能力的培养.

练习册系列答案
相关题目
 如图,过圆内接四边形ABCD的顶点C引圆的切线MN,AB为圆直径,若∠BCM=38°,则∠ABC=( )
如图,过圆内接四边形ABCD的顶点C引圆的切线MN,AB为圆直径,若∠BCM=38°,则∠ABC=( )| A、38° | B、52° |
| C、68° | D、42° |
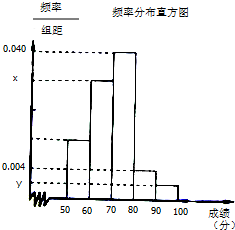 某中学举行了一次“环保知识竞赛”,全校学生参加了这次竞赛,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计.请根据下面尚未完成的频率分布表和频率分布直方图(如图所示)解决下列问题:
某中学举行了一次“环保知识竞赛”,全校学生参加了这次竞赛,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计.请根据下面尚未完成的频率分布表和频率分布直方图(如图所示)解决下列问题: 将边长为4的正方形ABCD和等腰直角三角形ABE按图拼为新的几何图形,△ABE中,AB=AE,连结DE,CE,若
将边长为4的正方形ABCD和等腰直角三角形ABE按图拼为新的几何图形,△ABE中,AB=AE,连结DE,CE,若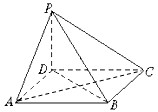 如图,四棱锥P-ABCD的底面ABCD为正方形,PD⊥底面ABCD,PD=AD.
如图,四棱锥P-ABCD的底面ABCD为正方形,PD⊥底面ABCD,PD=AD. 如图所示,△ABC内接于⊙O,AB=AC,直线XY切⊙O于点C,BD∥XY,AC、BD相交于E.
如图所示,△ABC内接于⊙O,AB=AC,直线XY切⊙O于点C,BD∥XY,AC、BD相交于E.