题目内容
某同学参加知识竞赛.需回答3个问题,规则如下:每题答对得100分,答错得-100分,假设这名同学每题答对的概率均为0.8,且各题答对与否相互没有影响.
(1)求这名同学回答这三个问题的总得分X的概率分布列
(2)求这名同学回答这三个问题的总得分X的数学期望.
(1)求这名同学回答这三个问题的总得分X的概率分布列
(2)求这名同学回答这三个问题的总得分X的数学期望.
考点:离散型随机变量的期望与方差,离散型随机变量及其分布列
专题:概率与统计
分析:由题意知这名同学回答这三个问题时可能三个题目都答对,答对两个、答对一个、答对0个,所以总得分ξ的可能取值是-300,-100,100,300.根据变量对应的事件根据独立重复试验公式得到结果.
解答:
解:(1):(Ⅰ)ξ的可能值为-300,-100,100,300.
P(ξ=-300)=0.23=0.008,P(ξ=-100)=3×0.22×0.8=0.096,
P(ξ=100)=3×0.2×0.82=0.384,P(ξ=300)=0.83=0.512,
所以ξ的概率分布为
(2)由ξ的分布列知:
Eξ=(-300)×0.08+(-100)×0.096+100×0.384+300×0.512=180.
P(ξ=-300)=0.23=0.008,P(ξ=-100)=3×0.22×0.8=0.096,
P(ξ=100)=3×0.2×0.82=0.384,P(ξ=300)=0.83=0.512,
所以ξ的概率分布为
| ξ | -300 | -100 | 100 | 300 |
| P | 0.008 | 0.096 | 0.384 | 0.512 |
Eξ=(-300)×0.08+(-100)×0.096+100×0.384+300×0.512=180.
点评:本小题主要考查离散型随机变量的分布列、数学期望等概念,以及运用概率统计知识解决实际问题的能力.这种题目高考必考,应注意解题的格式.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
若2,a,b,c,9成等差数列,则c-a的值为( )
| A、2.5 | B、3.5 |
| C、1.5 | D、3 |
已知a,b为非零实数,且a>b,则下列不等式成立的是( )
| A、a2b>ab2 | ||||
| B、a2>b2 | ||||
C、
| ||||
D、
|
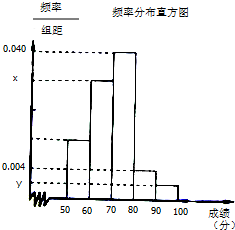 某中学举行了一次“环保知识竞赛”,全校学生参加了这次竞赛,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计.请根据下面尚未完成的频率分布表和频率分布直方图(如图所示)解决下列问题:
某中学举行了一次“环保知识竞赛”,全校学生参加了这次竞赛,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计.请根据下面尚未完成的频率分布表和频率分布直方图(如图所示)解决下列问题: 将边长为4的正方形ABCD和等腰直角三角形ABE按图拼为新的几何图形,△ABE中,AB=AE,连结DE,CE,若
将边长为4的正方形ABCD和等腰直角三角形ABE按图拼为新的几何图形,△ABE中,AB=AE,连结DE,CE,若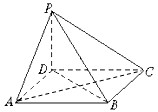 如图,四棱锥P-ABCD的底面ABCD为正方形,PD⊥底面ABCD,PD=AD.
如图,四棱锥P-ABCD的底面ABCD为正方形,PD⊥底面ABCD,PD=AD.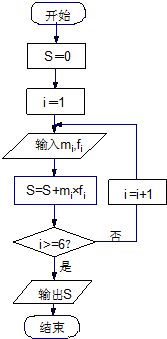 “世界睡眠日”定在每年的3月21日,2009年的世界睡眠日主题是“科学管理睡眠”,以提高公众对健康睡眠的自我管理能力和科学认识.为此某网站于2009年3月13日到3月20日持续一周网上调查公众日平均睡眠的时间(单位:小时),共有2000人参加调查,现将数据整理分组后如题中表格所示.
“世界睡眠日”定在每年的3月21日,2009年的世界睡眠日主题是“科学管理睡眠”,以提高公众对健康睡眠的自我管理能力和科学认识.为此某网站于2009年3月13日到3月20日持续一周网上调查公众日平均睡眠的时间(单位:小时),共有2000人参加调查,现将数据整理分组后如题中表格所示.