题目内容
过点P（3，2），且在两坐标轴上的截距相等的直线方程为（ ）
| A、2x-3y=0 |
| B、x+y-6=0 |
| C、x+y-5=0 |
| D、2x-3y=0或x+y-5=0 |
考点：直线的截距式方程
专题：直线与圆
分析：当直线过原点时，求出斜率，斜截式写出直线方程，并化为一般式．当直线不过原点时，设直线的方程为 x+y+m=0，把P（3，2）代入直线的方程，求出m值，可得直线方程．
解答：
解：当直线过原点时，斜率等于
=
，故直线的方程为y=
x．
当直线不过原点时，设直线的方程为 x+y+m=0，把P（3，2）代入直线的方程得 m=-5，
故求得的直线方程为 x+y-5=0，
综上，满足条件的直线方程为 y=
x或 x+y-5=0．
故选：D．
| 2-0 |
| 3-0 |
| 2 |
| 3 |
| 2 |
| 3 |
当直线不过原点时，设直线的方程为 x+y+m=0，把P（3，2）代入直线的方程得 m=-5，
故求得的直线方程为 x+y-5=0，
综上，满足条件的直线方程为 y=
| 2 |
| 3 |
故选：D．
点评：本题考查求直线方程的方法，待定系数法求直线的方程是一种常用的方法，体现了分类讨论的数学思想．
练习册系列答案
相关题目
如图在△ABC中，MN∥BC，MC，NB交于点O，则图中相似三角形的对数为（ ）
| A、1 | B、2 | C、3 | D、4 |
如图，过圆内接四边形ABCD的顶点C引圆的切线MN，AB为圆直径，若∠BCM=38°，则∠ABC=（ ）| A、38° | B、52° |
| C、68° | D、42° |
已知集合A={x|x2-x-6＜0}，B={x|x2+2x-8＞0}，则A∩B=（ ）
| A、{x|-3＜x＜-2} |
| B、{x|2＜x＜3} |
| C、{x|-4＜x＜-2或2＜x＜3} |
| D、{x|3＜x＜4} |
已知a，b为非零实数，且a＞b，则下列不等式成立的是（ ）
| A、a2b＞ab2 | ||||
| B、a2＞b2 | ||||
C、
| ||||
D、
|
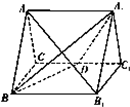如图，正三棱柱ABC-A1B1C1的所有棱长都为2，D为CC1中点．
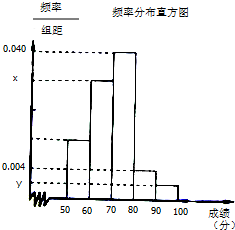某中学举行了一次“环保知识竞赛”，全校学生参加了这次竞赛，为了了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分取正整数，满分为100分）作为样本进行统计．请根据下面尚未完成的频率分布表和频率分布直方图（如图所示）解决下列问题：
将边长为4的正方形ABCD和等腰直角三角形ABE按图拼为新的几何图形，△ABE中，AB=AE，连结DE，CE，若