题目内容
已知函数y=2a+bsinx的最大值为3 最小值为1,则函数y=-4asin
x的最小正周期为 .
| b |
| 2 |
考点:三角函数的周期性及其求法
专题:三角函数的图像与性质
分析:根据三角函数的最值求出a,b的值,然后利用三角函数的周期公式即可得到结论.
解答:
解:∵函数y=2a+bsinx的最大值为3 最小值为1,若b>0,
则
,解得a=1,b=1,
∴函数y=-4asin
x的最小正周期T=
=
=
=4π,
若b<0,则
,解得a=1,b=-1,
函数y=-4asin
x=-4sin(-
x)=4sin
x,
则函数的周期T=
=4π
故答案为:π或4π
则
|
∴函数y=-4asin
| b |
| 2 |
| 2π | ||
|
| 4π |
| b |
| 4π |
| 1 |
若b<0,则
|
函数y=-4asin
| b |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
则函数的周期T=
| 2π | ||
|
故答案为:π或4π
点评:本题主要考查三角函数周期的求法,根据三角函数的最值求出a,b是解决本题的关键,比较基础.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
“m=n”是“方程mx2+ny2=1表示圆”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
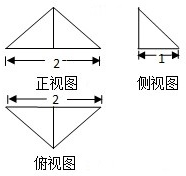 一个几何体的三视图及部分数据如图所示,正视图、侧视图和俯视图都是等腰直角三角形,则该几何体的外接球体积为
一个几何体的三视图及部分数据如图所示,正视图、侧视图和俯视图都是等腰直角三角形,则该几何体的外接球体积为