题目内容
台风中心从A地以每小时20千米的速度向东北方向移动，离台风中心30千米的地区为危险区，城市B在A地正东40千米处，则城市B处在危险区内的时间是 ．
考点：圆方程的综合应用
专题：综合题,直线与圆
分析：先以A为坐标原点，建立平面直角坐标系，进而可知B点坐标和台风中心移动的轨迹，求得点B到射线的距离，进而求得答案．
解答：
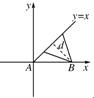解：如图，以A为坐标原点，建立平面直角坐标系，A（0，0）B（40，0），r=30，
圆B（x-40）2+y2=302．
台风中心移到圆B内时，B城处于危险，台风移动所在直线是y=x，交圆B于M，N
点B到射线y=x的距离d=
=20
，
得|MN|=2
=20，
所以
=1，所以B城处于危险的时间是1小时．
故答案为：1小时．
解：如图，以A为坐标原点，建立平面直角坐标系，A（0，0）B（40，0），r=30，圆B（x-40）2+y2=302．
台风中心移到圆B内时，B城处于危险，台风移动所在直线是y=x，交圆B于M，N
点B到射线y=x的距离d=
| 40 | ||
|
| 2 |
得|MN|=2
| 900-800 |
所以
| |MN| |
| 2 |
故答案为：1小时．
点评：本题主要考查了解三角形的实际应用．通过建立直角坐标系把三角形问题转换成解析几何的问题，方便了问题的解决．
练习册系列答案
相关题目
关于平面向量
，
，
，有下列三个命题：
①若
•
=
•
，则
=
；
②若
=（1，k），
=（-2，6），
∥
，则k=-3；
③非零向量a和b满足|
|=|
|=|
-
|，则
与
+
的夹角为30°．其中真命题的序号为（ ）
| a |
| b |
| c |
①若
| a |
| b |
| a |
| c |
| b |
| c |
②若
| a |
| b |
| a |
| b |
③非零向量a和b满足|
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| A、①② | B、①③ | C、②③ | D、①②③ |
直线x=2与双曲线
-y2=1的渐近线交于A、B两点，设P为双曲线上的任意一点，若
=a
+b
（a，b∈R，O为坐标原点），则a、b满足的关系是（ ）
| x2 |
| 4 |
| OP |
| OA |
| OB |
A、ab=
| ||
B、ab=
| ||
C、a2+b2=
| ||
D、a2+b2=
|