题目内容
如图，四棱锥S-ABCD的底面为正方形，SD⊥底面ABCD，则下列结论中不正确的是（ ）
| A、AC⊥SB |
| B、AB∥平面SCD |
| C、AB与SC所成的角等于DC与SA所成的角 |
| D、SA与平面SBD所成的角等于SC与平面SBD所成的角 |
考点：命题的真假判断与应用
专题：空间位置关系与距离
分析：A．利用正方形的性质和线面垂直的性质与判定即可得出；
B．利用正方形的性质和线面平行的判定定理即可得出；
C．通过平移即可得出异面直线所成的角；
D．利用线面垂直的判定与性质、线面角的定义、等腰三角形的性质即可得出．
B．利用正方形的性质和线面平行的判定定理即可得出；
C．通过平移即可得出异面直线所成的角；
D．利用线面垂直的判定与性质、线面角的定义、等腰三角形的性质即可得出．
解答：
解：A．∵SD⊥平面ABCD，∴SD⊥AC．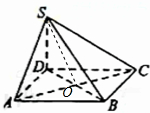
∵四边形ABCD是正方形，∴AC⊥BD．
又∵SD∩DB=D．
∴AC⊥平面SDB，∴AC⊥DB．
B．∵四边形ABCD是正方形，∴AB∥DC，
又AB?平面SCD，CD?平面SCD，
∴AB∥平面SCD．
C．∵AB∥DC，∴∠SCD（为锐角）是AB与SC所成的角，∠SAB（为直角）是DC与SA所成的角；
而∠SCD≠∠SAB．
∴AB与SC所成的角等于DC与SA所成的角不正确；
D．由A可知：AC⊥平面SDB，∴∠ASO、∠SCO分别是SA与平面SBD所成的角、SC与平面SBD所成的角．
由SA=SC，OA=OC，可得∠ASO=∠SCO，因此正确．
综上可知：只有C不正确．
故选：C．
∵四边形ABCD是正方形，∴AC⊥BD．
又∵SD∩DB=D．
∴AC⊥平面SDB，∴AC⊥DB．
B．∵四边形ABCD是正方形，∴AB∥DC，
又AB?平面SCD，CD?平面SCD，
∴AB∥平面SCD．
C．∵AB∥DC，∴∠SCD（为锐角）是AB与SC所成的角，∠SAB（为直角）是DC与SA所成的角；
而∠SCD≠∠SAB．
∴AB与SC所成的角等于DC与SA所成的角不正确；
D．由A可知：AC⊥平面SDB，∴∠ASO、∠SCO分别是SA与平面SBD所成的角、SC与平面SBD所成的角．
由SA=SC，OA=OC，可得∠ASO=∠SCO，因此正确．
综上可知：只有C不正确．
故选：C．
点评：本题综合考查了空间位置关系和空间角、正方形的性质，属于中档题．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
变量x，y满足约束条件
，则x+3y最大值是（ ）
|
| A、2 | B、3 | C、4 | D、5 |
下面给出四个命题：
①若a≥b＞-1，则
≥
；
②a＜-1是一元二次方程ax2+2x+1=0有一个正根和一个负根的充分不必要条件；
③在数列{an}中，a1＜a2＜a3是数列{an}为递增数列的必要不充分条件；
④方程(x+y-2)
=0表示的曲线是一个圆和一条直线．
其中为真命题的是（ ）
①若a≥b＞-1，则
| a |
| 1+a |
| b |
| 1+b |
②a＜-1是一元二次方程ax2+2x+1=0有一个正根和一个负根的充分不必要条件；
③在数列{an}中，a1＜a2＜a3是数列{an}为递增数列的必要不充分条件；
④方程(x+y-2)
| x2+y2-9 |
其中为真命题的是（ ）
| A、①②③ | B、①③④ |
| C、②④ | D、①②③④ |
设△ABC是边长为1的正三角形，点P1，P2，P3四等分线段BC（如图所示）．