题目内容
设变量x,y满足约束条件
,且目标函数z=kx+2y的最大值为4,且取得最大值的最优解有无穷多个,则k的值为( )
|
| A、-2 | ||
| B、1 | ||
C、-
| ||
D、
|
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,根据目标函数的最大值以及取得最大值的最优解有无穷多个,得到目标函数的斜率的关系即可得到结论.
解答:
解:作出不等式组对应的平面区域如图:
∵目标函数z=kx+2y的最大值为4,且取得最大值的最优解有无穷多个,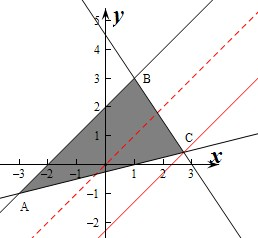
∴kx+2y=4,此时y=-
x+2,
则直线y=-
x+2的斜率必与其中一条直线的斜率相等,且对应图象在直线y=-
x+2的上方,
由图象可知直线y=-
x+2的斜率-
=kAB,
即-
=1,
解得k=-2,
故选:A.
∵目标函数z=kx+2y的最大值为4,且取得最大值的最优解有无穷多个,

∴kx+2y=4,此时y=-
| k |
| 2 |
则直线y=-
| k |
| 2 |
| k |
| 2 |
由图象可知直线y=-
| k |
| 2 |
| k |
| 2 |
即-
| k |
| 2 |
解得k=-2,
故选:A.
点评:本题主要考查线性规划的应用,根据目标函数的取值范围得到目标斜率的取值关系是解决本题的关键,要注意使用数形结合的数学思想.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
对于平面α,β,γ和直线a,b,m,n,下列命题中真命题是( )
| A、若a⊥m,a⊥n,m?α,n?α,则a⊥α |
| B、若α∥β,α∩γ=a,β∩γ=b,则a∥b |
| C、若a∥b,b?α,则a∥α |
| D、若a?β,b?β,a∥α,b∥α,则β∥α. |
如图,四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中不正确的是( )


| A、AC⊥SB |
| B、AB∥平面SCD |
| C、AB与SC所成的角等于DC与SA所成的角 |
| D、SA与平面SBD所成的角等于SC与平面SBD所成的角 |
双曲线x2-y2=4左支上一点P(a,b)到直线y=x的距离为
,则a+b=( )
| 2 |
| A、-2 | B、2 | C、-4 | D、4 |