题目内容
下列四个命题:
①函数y=-
在其定义域上是增函数;
②y=x和y=
表示同一个函数;
③y=x2-2|x|-3的递增区间为[1,+∞);
④若2a=3b<1,则a<b<0.
其中正确命题的序号是 .
①函数y=-
| 1 |
| x |
②y=x和y=
| x2 |
③y=x2-2|x|-3的递增区间为[1,+∞);
④若2a=3b<1,则a<b<0.
其中正确命题的序号是
考点:命题的真假判断与应用
专题:综合题,函数的性质及应用
分析:①利用y=-
的单调性质可判断①之正误;
②利用y=
=|x|可判断y=x和y=
是否为同一函数;
③通过对x范围的讨论,利用二次函数的单调性质可求得y=x2-2|x|-3的递增区间,从而可判断其正误;
④在同一直角坐标系中作出y=3x与y=2x的图象,数形结合,可判断④之正误.
| 1 |
| x |
②利用y=
| x2 |
| x2 |
③通过对x范围的讨论,利用二次函数的单调性质可求得y=x2-2|x|-3的递增区间,从而可判断其正误;
④在同一直角坐标系中作出y=3x与y=2x的图象,数形结合,可判断④之正误.
解答:
解:①∵y=-
在区间(-∞,0),(0,+∞)上单调递增,但在其定义域内并不是增函数,故①错误;
②∵y=
=|x|,显然与y=x不是同一函数,故②错误;
③令f(x)=x2-2|x|-3,
则f(-x)=(-x)2-2|-x|-3=x2-2|x|-3=f(x),故f(x)=x2-2|x|-3为偶函数,
又当x≥0时,f(x)=x2-2x-3=(x-1)2-4,在区间[0,1]上单调递减,在区间[1,+∞)上单调递增,而偶函数在对称区间上的单调性相反,
∴y=x2-2|x|-3的递增区间为[-1,0],[1,+∞),故③错误;
④在同一直角坐标系中作出y=3x与y=2x的图象,
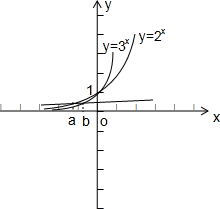
∵2a=3b<1,
由图知a<b<0,故④正确;
综上所述,正确命题的序号是④.
故答案为:④.
| 1 |
| x |
②∵y=
| x2 |
③令f(x)=x2-2|x|-3,
则f(-x)=(-x)2-2|-x|-3=x2-2|x|-3=f(x),故f(x)=x2-2|x|-3为偶函数,
又当x≥0时,f(x)=x2-2x-3=(x-1)2-4,在区间[0,1]上单调递减,在区间[1,+∞)上单调递增,而偶函数在对称区间上的单调性相反,
∴y=x2-2|x|-3的递增区间为[-1,0],[1,+∞),故③错误;
④在同一直角坐标系中作出y=3x与y=2x的图象,

∵2a=3b<1,
由图知a<b<0,故④正确;
综上所述,正确命题的序号是④.
故答案为:④.
点评:本题考查命题的真假判断与应用,着重考查函数的单调性与图象性质,考查作图能力、分析解决问题的能力,属于中档题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
下列古典概型的说法中正确的个数是( )
①试验中所有可能出现的基本事件只有有限个;
②每个事件出现的可能性相等;
③基本事件的总数为n,随机事件A包含k个基本事件,则P(A)=
;
④每个基本事件出现的可能性相等.
①试验中所有可能出现的基本事件只有有限个;
②每个事件出现的可能性相等;
③基本事件的总数为n,随机事件A包含k个基本事件,则P(A)=
| k |
| n |
④每个基本事件出现的可能性相等.
| A、1 | B、2 | C、3 | D、4 |
如图,四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中不正确的是( )


| A、AC⊥SB |
| B、AB∥平面SCD |
| C、AB与SC所成的角等于DC与SA所成的角 |
| D、SA与平面SBD所成的角等于SC与平面SBD所成的角 |
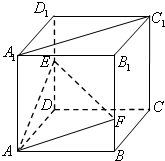 如图,在棱长为a的正方体ABCD-A1B1C1D1中,点E是棱D1D的中点,点F在棱B1B上,且满足B1F=2FB.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,点E是棱D1D的中点,点F在棱B1B上,且满足B1F=2FB.