题目内容
15.设$f(x)=\left\{\begin{array}{l}{x^2}({0≤x<1})\\ 2-x({1≤x≤2})\end{array}\right.$则$\int_0^2{f(x)}dx$等于( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{5}$ | C. | $\frac{5}{6}$ | D. | 不存在 |
分析 根据定积分的计算法则计算即可.
解答 解:设$f(x)=\left\{\begin{array}{l}{x^2}({0≤x<1})\\ 2-x({1≤x≤2})\end{array}\right.$
则$\int_0^2{f(x)}dx$=${∫}_{0}^{1}$x2dx+${∫}_{1}^{2}$(2-x)dx=$\frac{1}{3}$x3|${\;}_{0}^{1}$+(2x-$\frac{1}{2}$x2)|${\;}_{1}^{2}$=$\frac{1}{3}$+(4-2)-(2-$\frac{1}{2}$)=$\frac{5}{6}$,
故选:C
点评 本题考查了分段函数和定积分的计算,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.已知正项等比数列{an}的前n项和为Sn,且4a2=a4,则$\frac{S_4}{{{a_2}+{a_5}}}$等于( )
| A. | $\frac{5}{6}$ | B. | $\frac{5}{7}$ | C. | $\frac{3}{4}$ | D. | $\frac{7}{9}$ |
20.一次单元测验由20个选择题构成,每个选择题有4个选项,其中有且仅有一个选项是正确答案,每题选择正确答案得5分,不作出选择或选错不得分,满分100分.学生甲选对任一题的概率为0.9,学生乙则在测验中对每题都从4个选择中随机地选择一个,求学生甲和乙在这次测验中成绩的均值分别为( )
| A. | 18,5 | B. | 18,25 | C. | 90,25 | D. | 90,5 |
7.棱长为4的正方体的内切球的表面积为( )
| A. | 4π | B. | 12π | C. | 16π | D. | 20π |
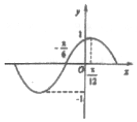 函数f(x)=sin(ωx+φ)(ω<0,|φ|<$\frac{π}{2}$)的部分图象如图所示,将y=f(x)的图象向右平移$\frac{π}{4}$个单位长度后得到函数y=g(x)的图象.
函数f(x)=sin(ωx+φ)(ω<0,|φ|<$\frac{π}{2}$)的部分图象如图所示,将y=f(x)的图象向右平移$\frac{π}{4}$个单位长度后得到函数y=g(x)的图象.