题目内容
13.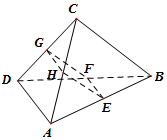 (理科)如图,在空间四面体ABCD中,若E,F,G,H分别是AB,BD,CD,AC的中点,且AD⊥BC
(理科)如图,在空间四面体ABCD中,若E,F,G,H分别是AB,BD,CD,AC的中点,且AD⊥BC(1)求证:四边形EFGH是矩形.
(2)求证:AD∥平面EFGH.
分析 (1)推导出EF$\underset{∥}{=}$$\frac{1}{2}AD$,GH$\underset{∥}{=}$$\frac{1}{2}AD$,从而EF$\underset{∥}{=}$GH,由此能证明四边形EFGH是平行四边形,再由AD⊥BC,得EF⊥GF,从而四边形EFGH是矩形.
(2)推导出EF∥AD,由此能证明BC∥平面EFGH.
解答 证明:(1)∵在空间四面体ABCD中,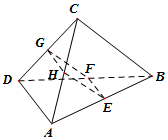
E,F,G,H分别是AB,BD,CD,AC的中点,
∴EF$\underset{∥}{=}$$\frac{1}{2}AD$,GH$\underset{∥}{=}$$\frac{1}{2}AD$,
∴EF$\underset{∥}{=}$GH,
∴四边形EFGH是平行四边形,
∵E,F分别是AB,DB的中点,∴EF∥AD,
∵G,F分别是DC,DB的中点,∴GF∥BC,
∵AD⊥BC,∴EF⊥GF,
∴四边形EFGH是矩形.
(2)∵E,F分别是AB,DB的中点,∴EF∥AD,
∵EF?平面EFGH,AD?平面EFGH,
∴AD∥平面EFGH.
点评 本题考查四边形是矩形的证明,考查线面平行的证明,考查推理论证能力、运算求解能力、空间思维能力,考查转化化归思想、数形结合思想,是基础题.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
8.某同学的父亲决定今年夏天卖西瓜赚钱,根据去年6月份的数据统计连续五天内每天所卖西瓜的个数与温度之间的关系如表:
(1)求这五天内所卖西瓜个数的平均值和方差;
(2)求变量x.y之间的线性回归方程,并预测当温度为30℃时所卖西瓜的个数.
附:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$(精确到0.1)
| 温度x(℃) | 32 | 33 | 35 | 37 | 38 |
| 西瓜个数y | 20 | 22 | 24 | 30 | 34 |
(2)求变量x.y之间的线性回归方程,并预测当温度为30℃时所卖西瓜的个数.
附:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}•\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$(精确到0.1)
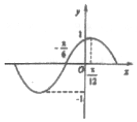 函数f(x)=sin(ωx+φ)(ω<0,|φ|<$\frac{π}{2}$)的部分图象如图所示,将y=f(x)的图象向右平移$\frac{π}{4}$个单位长度后得到函数y=g(x)的图象.
函数f(x)=sin(ωx+φ)(ω<0,|φ|<$\frac{π}{2}$)的部分图象如图所示,将y=f(x)的图象向右平移$\frac{π}{4}$个单位长度后得到函数y=g(x)的图象.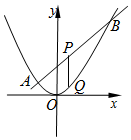 已知抛物线C:x2=2py(p>0)的焦点为F,直线2x-y+2=0交抛物线C于A,B两点,P是线段AB的中点,过P作x轴的垂线交抛物线C于点Q.
已知抛物线C:x2=2py(p>0)的焦点为F,直线2x-y+2=0交抛物线C于A,B两点,P是线段AB的中点,过P作x轴的垂线交抛物线C于点Q.