题目内容
10.已知矩形ABCD中,AB=6,BC=4,E,F分别是AB,CD上两动点,且AE=DF,把四边形BCFE沿EF折起,使平面BCFE⊥平面ABCD,若折得的几何体的体积最大,则该几何体外接球的体积为( )| A. | 28π | B. | $\frac{{28\sqrt{7}π}}{3}$ | C. | 32π | D. | $\frac{{64\sqrt{2}π}}{3}$ |
分析 三棱柱ABE-DCF的底面积最大时,其体积最大.设FC=x,DCF=6-x,s△DCF=$\frac{1}{2}×FC×CD$=$\frac{1}{2}x\sqrt{(6-x)^{2}-{x}^{2}}=\frac{1}{2}x•\sqrt{36-12x}$=$\frac{1}{2}×\sqrt{36{x}^{2}-12{x}^{3}}$.令f(x)=36x2-12x3,f′(x)=72x-36x2,令f(x)=0,可得x=2,即当x=2时,
s△DCF最大,此时CF,CD,CB两两垂直,可以把此三棱柱补成长方体,外接球的半径为长方体对角线长的一半,得球半径R即可.
解答 解: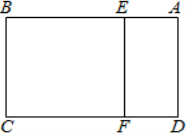
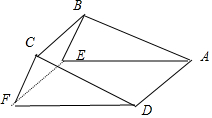
将矩形ABCD沿EF折起,使得平面ABCD⊥平面BCFE,可得直三棱柱ABE-DCF,(如图)
三棱柱ABE-DCF的底面△DCF,△ABE是直角△,AB⊥BE,FC⊥CD
三棱柱ABE-DCF的底面积最大时,其体积最大.
设FC=x,DCF=6-x,s△DCF=$\frac{1}{2}×FC×CD$=$\frac{1}{2}x\sqrt{(6-x)^{2}-{x}^{2}}=\frac{1}{2}x•\sqrt{36-12x}$=$\frac{1}{2}×\sqrt{36{x}^{2}-12{x}^{3}}$.
令f(x)=36x2-12x3,f′(x)=72x-36x2,令f(x)=0,可得x=2
∴当x=2时,s△DCF最大
此时CF,CD,CB两两垂直,可以把此三棱柱补成长方体,外接球的半径为长方体对角线长的一半
球半径R=$\frac{1}{2}\sqrt{{4}^{2}+(2\sqrt{3})^{2}+{2}^{2}}=2\sqrt{2}$,∴几何体外接球的体积为$\frac{4}{3}π{R}^{3}=\frac{64\sqrt{2}}{3}π$,
故选:D.
点评 本题考查了折叠问题,及三棱柱的外接球,属于中档题.

 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案| A. | 18,5 | B. | 18,25 | C. | 90,25 | D. | 90,5 |
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
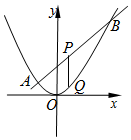 已知抛物线C:x2=2py(p>0)的焦点为F,直线2x-y+2=0交抛物线C于A,B两点,P是线段AB的中点,过P作x轴的垂线交抛物线C于点Q.
已知抛物线C:x2=2py(p>0)的焦点为F,直线2x-y+2=0交抛物线C于A,B两点,P是线段AB的中点,过P作x轴的垂线交抛物线C于点Q.