题目内容
14.已知$\overrightarrow{a}$=($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),|$\overrightarrow{b}$|=1,|$\overrightarrow{a}$+2$\overrightarrow{b}$|=2,则$\overrightarrow b$在$\overrightarrow a$方向上的投影为-$\frac{1}{4}$.分析 运用向量模的公式和向量的平方即为模的平方,可得$\overrightarrow{a}$•$\overrightarrow{b}$,再由$\overrightarrow b$在$\overrightarrow a$方向上的投影为$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|}$,计算即可得到所求.
解答 解:$\overrightarrow{a}$=($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),|$\overrightarrow{b}$|=1,|$\overrightarrow{a}$+2$\overrightarrow{b}$|=2,
可得|$\overrightarrow{a}$|=1,|$\overrightarrow{a}$+2$\overrightarrow{b}$|2=4,
即为$\overrightarrow{a}$2+4$\overrightarrow{a}$•$\overrightarrow{b}$+4$\overrightarrow{b}$2=4,
即有1+4$\overrightarrow{a}$•$\overrightarrow{b}$+4=4,
$\overrightarrow{a}$•$\overrightarrow{b}$=-$\frac{1}{4}$,
可得$\overrightarrow b$在$\overrightarrow a$方向上的投影为$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|}$=-$\frac{1}{4}$.
故答案为:-$\frac{1}{4}$.
点评 本题考查向量数量积的性质:向量的平方即为模的平方,考查向量的投影概念,运算求解能力,属于基础题.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
| A. | a=$\sqrt{3}$ | B. | a=-$\sqrt{3}$ | C. | a=-1 | D. | a=1 |
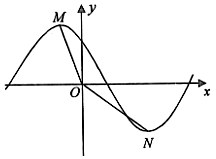 将函数y=$\sqrt{3}$sin($\frac{π}{4}$x)的图象向左平移3个单位,得函数y=$\sqrt{3}$sin($\frac{π}{4}$x+φ)(|φ|<π)的图象(如图),点M,N分别是函数f(x)图象上y轴两侧相邻的最高点和最低点,设∠MON=θ,则tan(φ-θ)的值为( )
将函数y=$\sqrt{3}$sin($\frac{π}{4}$x)的图象向左平移3个单位,得函数y=$\sqrt{3}$sin($\frac{π}{4}$x+φ)(|φ|<π)的图象(如图),点M,N分别是函数f(x)图象上y轴两侧相邻的最高点和最低点,设∠MON=θ,则tan(φ-θ)的值为( )| A. | 1-$\sqrt{3}$ | B. | 2-$\sqrt{3}$ | C. | 1+$\sqrt{3}$ | D. | -2+$\sqrt{3}$ |
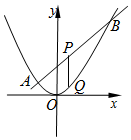 已知抛物线C:x2=2py(p>0)的焦点为F,直线2x-y+2=0交抛物线C于A,B两点,P是线段AB的中点,过P作x轴的垂线交抛物线C于点Q.
已知抛物线C:x2=2py(p>0)的焦点为F,直线2x-y+2=0交抛物线C于A,B两点,P是线段AB的中点,过P作x轴的垂线交抛物线C于点Q.