题目内容
10.(1-x)(2x+1)5中,x3项的系数为40.(用数字作答)分析 (1-x)(2x+1)5中x3项的系数,前一个括号里取1,后面的取x3,或者前一个括号里取x,后面的取x2,问题得以解决.
解答 解:(1-x)(2x+1)5中x3项的系数,前一个括号里取1,后面的取x3,或者前一个括号里取x,后面的取x2,
故x3项的系数为23C53-22C52=80-40=40,
故答案为:40.
点评 本题考查了二项式定理的应用问题,也考查了利用展开式的通项公式求指定项的系数,是基础题

练习册系列答案
相关题目
20.实数x、y满足3x2+4y2=12,则z=2x+$\sqrt{3}y$的最小值是( )
| A. | -5 | B. | -6 | C. | 3 | D. | 4 |
19.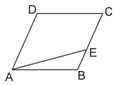 已知菱形ABCD中,∠A=$\frac{π}{3}$,AB=1,E为BC边上任一点,则$\overrightarrow{AE}$•$\overrightarrow{EC}$的最大值为( )
已知菱形ABCD中,∠A=$\frac{π}{3}$,AB=1,E为BC边上任一点,则$\overrightarrow{AE}$•$\overrightarrow{EC}$的最大值为( )
 已知菱形ABCD中,∠A=$\frac{π}{3}$,AB=1,E为BC边上任一点,则$\overrightarrow{AE}$•$\overrightarrow{EC}$的最大值为( )
已知菱形ABCD中,∠A=$\frac{π}{3}$,AB=1,E为BC边上任一点,则$\overrightarrow{AE}$•$\overrightarrow{EC}$的最大值为( )| A. | $\frac{1}{3}$ | B. | $\frac{9}{16}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{5}$ |
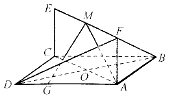 如图,已知正方形ABCD和矩形ACEF所在平面相互垂直,AB=$\sqrt{2}$,AF=1,G为线段AD上的任意一点.
如图,已知正方形ABCD和矩形ACEF所在平面相互垂直,AB=$\sqrt{2}$,AF=1,G为线段AD上的任意一点.