题目内容
1．设集合U={1，2，3，4，5}，从集合U中选4个数，组成没有重复数字的四位数，并且此四位数大于2345，同时小于4351，则满足条件的四位数共有54．分析 由题意可以分为四类，根据分类计数原理可得．
解答 解：第一类：若千位数字为3，其它数字任意排列，有A43=24种，
第二类：若千位数字为2，百位数字为4和5选一个，其它数字任意排列共有A21A32=12种，
第三类：若千位数字为2，百位数字为3，则十位数字只能为5，个位数字任意排列共有2种，
第三类：若千位数字为4，百位数字为1和2选一个，其它数字任意排列共有A21A32=12种，
第四类：若千位数字为4，百位数字为3，则十位数字从2或1选一个，个位数字任意排列共有2×2=4种，
根据分类计数原理可得，共有24+12+2+12+4=54种，
故答案为：54．
点评 本题考查了分类计数原理，关键是特殊位置特殊安排，属于中档题
练习册系列答案
同步练习强化拓展系列答案
相关题目
16．已知m，n，l是三条不同的直线，α，β是两个不同的平面，下列命题正确的是（ ）
| A． | 若m∥α，n⊥β，m⊥n，则α⊥β | B． | 若m?α，n?α，n⊥l，则l⊥α | ||
| C． | 若m∥α，n⊥β，α⊥β，则m∥n | D． | 若l⊥α，l⊥β，则α∥β |
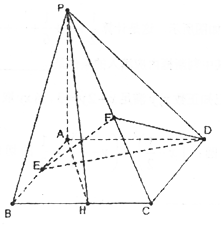如图，四棱锥P-ABCD的底面为正方形，侧面PAD⊥底面ABCD，PA⊥AD，E，F，H分别为AB，PC，BC的中点．