题目内容
9.在等差数列{an}中,已知a1=2,S9=54,若数列{$\frac{1}{{a}_{n}{a}_{n+1}}$}的前n项和为$\frac{7}{16}$,则n=14.分析 利用等差数列性质求出公差d=1,从而an=n+1,进而$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{n+1}-\frac{1}{n+2}$,由此根据数列{$\frac{1}{{a}_{n}{a}_{n+1}}$}的前n项和为$\frac{7}{16}$,利用裂项求和法能求出n的值.
解答 解:∵在等差数列{an}中,a1=2,S9=54,
∴$9×2+\frac{9×8}{2}d=54$,解得d=1,
∴an=2+n-1=n+1,
∴$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{(n+1)(n+2)}$=$\frac{1}{n+1}-\frac{1}{n+2}$,
∵数列{$\frac{1}{{a}_{n}{a}_{n+1}}$}的前n项和为$\frac{7}{16}$,
∴$\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+…+\frac{1}{n+1}-\frac{1}{n+2}$=$\frac{7}{16}$,
∴$\frac{1}{2}$-$\frac{1}{n+2}$=$\frac{7}{16}$,
解得n=14.
故答案为:14.
点评 本题考查等差数列的项数n的求法,是基础题,解题时要认真审题,注意等差数列的通项公式、前n项和公式、裂项求和法的合理运用.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
19.函数f(x)的图象如图所示,则下列结论正确的是( )
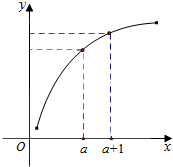

| A. | 0<f′(a)<f′(a+1)<f(a+1)-f(a) | B. | 0<f′(a+1)<f(a+1)-f(a)<f′(a) | ||
| C. | 0<f′(a+1)<f′(a)<f(a+1)-f(a) | D. | 0<f(a+1)-f(a)<f′(a)<f′(a+1) |
17.如图,在平行四边形ABCD中,E为BC的中点,且$\overrightarrow{DE}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$,则( )
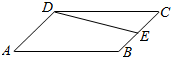

| A. | x=-1,y=-$\frac{1}{2}$ | B. | x=1,y=$\frac{1}{2}$ | C. | x=-1,y=$\frac{1}{2}$ | D. | x=1,y=-$\frac{1}{2}$ |
14.设函数f(x)=$\left\{\begin{array}{l}{(\frac{1}{2})^{x},x≥0}\\{f(-x),x<0}\end{array}\right.$,则f(log2$\frac{1}{6}$)=( )
| A. | -$\frac{1}{6}$ | B. | -6 | C. | 6 | D. | $\frac{1}{6}$ |
18.若m>n,则( )
| A. | 0.2m<0.2n | B. | log0.3m>log0.3n | C. | 2m<2n | D. | m2>n2 |
19.已知数列$\frac{1}{1×2},\frac{1}{2×3},\frac{1}{3×4},…,\frac{1}{{n×({n+1})}},…$,下面各数中是此数列中的项的是( )
| A. | $\frac{1}{35}$ | B. | $\frac{1}{42}$ | C. | $\frac{1}{48}$ | D. | $\frac{1}{54}$ |
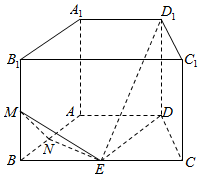 如图,直四棱柱ABCD-A1B1C1D1的底面是等腰梯形,AB=CD=AD=1,BC=2,E,M,N分别是所在棱的中点.
如图,直四棱柱ABCD-A1B1C1D1的底面是等腰梯形,AB=CD=AD=1,BC=2,E,M,N分别是所在棱的中点.