题目内容
8.已知点P(0,2)和圆C:x2+y2-8x+11=0.(1)求过点P,点C和原点三点圆的方程;
(2)求以点P为圆心且与圆C外切的圆的方程.
分析 (1)化圆C的方程为标准方程,求出圆C的圆心坐标和半径,再设过点P,点C和原点三点圆的方程为x2+y2+Dx+Ey+F=0.代入点的坐标可得关于D、E、F的三元一次方程组,求出D、E、F的值得所求圆的方程;
(2)求出P与C的距离,减去已知圆的半径得到要求圆的半径,代入圆的标准方程得答案.
解答 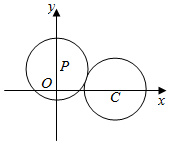 解:(1)化圆C:x2+y2-8x+11=0为(x-4)2+y2=5
解:(1)化圆C:x2+y2-8x+11=0为(x-4)2+y2=5
则圆心C(4,0),半径r=$\sqrt{5}$,
设过点P,点C和原点三点圆的方程为x2+y2+Dx+Ey+F=0.
代入点的坐标得:$\left\{\begin{array}{l}{F=0}\\{{2}^{2}+2E+F=0}\\{{4}^{2}+4D+F=0}\end{array}\right.$,即$\left\{\begin{array}{l}{F=0}\\{2E+F+4=0}\\{4D+F+16=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{D=-4}\\{E=-2}\\{F=0}\end{array}\right.$.
∴过点P,点C和原点三点圆的方程为x2+y2-4x-2y=0;
(2)如图,∵C(4,0),P(0,2),
∴|PC|=$\sqrt{(4-0)^{2}+(0-2)^{2}}=2\sqrt{5}$,
又圆C的半径r=$\sqrt{5}$,且圆P与圆C外切,
∴圆P的半径为$2\sqrt{5}-\sqrt{5}=\sqrt{5}$.
则以点P为圆心且与圆C外切的圆的方程为x2+(y-2)2=5.
点评 本题考查圆的一般式方程,考查了圆与圆位置关系的应用,是中档题.

练习册系列答案
相关题目
19.双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的一条渐近线方程为y=2x,则C的离心率是( )
| A. | $\sqrt{5}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $\frac{{\sqrt{5}}}{2}$ |
16.设单位向量$\overrightarrow{e_1}$与$\overrightarrow{e_2}$既不平行也不垂直,对非零向量$\overrightarrow a={x_1}\overrightarrow{e_1}+{y_1}\overrightarrow{e_2}$、$\overrightarrow b={x_2}\overrightarrow{e_1}+{y_2}\overrightarrow{e_2}$有结论:
①若x1y2-x2y1=0,则$\overrightarrow a∥\overrightarrow b$;
②若x1x2+y1y2=0,则$\overrightarrow a⊥\overrightarrow b$.
关于以上两个结论,正确的判断是( )
①若x1y2-x2y1=0,则$\overrightarrow a∥\overrightarrow b$;
②若x1x2+y1y2=0,则$\overrightarrow a⊥\overrightarrow b$.
关于以上两个结论,正确的判断是( )
| A. | ①成立,②不成立 | B. | ①不成立,②成立 | C. | ①成立,②成立 | D. | ①不成立,②不成立 |
13.设a=${∫}_{0}^{π}$$\sqrt{2}$cos(x-$\frac{π}{4}$)dx,则二项式(a$\sqrt{x}$-$\frac{1}{\sqrt{x}}$)4中展开式中含x项的系数是( )
| A. | -32 | B. | 32 | C. | -8 | D. | 8 |