题目内容
3.已知$3{cos^2}({π+x})+5cos({\frac{π}{2}-x})=1$,则tanx=$\frac{{\sqrt{2}}}{4}$或$-\frac{{\sqrt{2}}}{4}$.分析 利用诱导公式,同角三角函数基本关系式化简已知可得3sin2x-5sinx-2=0,从而解得sinx的值,进而利用同角三角函数基本关系式可求cosx,tanx的值.
解答 解:∵$3{cos^2}({π+x})+5cos({\frac{π}{2}-x})=1$,化简可得:3cos2x+5sinx=1,
∴3sin2x-5sinx-2=0,
∴解得:sinx=2(舍去)或-$\frac{1}{3}$,
∴cosx=±$\sqrt{1-si{n}^{2}x}$=±$\frac{2\sqrt{2}}{3}$,
∴tanx=$\frac{sinx}{cosx}$=$\frac{{\sqrt{2}}}{4}$或$-\frac{{\sqrt{2}}}{4}$.
故答案为:$\frac{{\sqrt{2}}}{4}$或$-\frac{{\sqrt{2}}}{4}$.
点评 本题主要考查了诱导公式,同角三角函数基本关系式在三角函数化简求值中的应用,考查了计算能力和转化思想,属于基础题.

练习册系列答案
相关题目
13.已知i是虚数单位,则i(1-i)2=( )
| A. | 2-2i | B. | 2+2i | C. | -2 | D. | 2 |
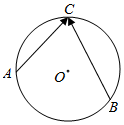 如图,⊙O是以O为圆心、1为半径的圆,设点A,B,C为⊙O上的任意三点,则$\overrightarrow{AC}$•$\overrightarrow{BC}$的取值范围为[-4,4].
如图,⊙O是以O为圆心、1为半径的圆,设点A,B,C为⊙O上的任意三点,则$\overrightarrow{AC}$•$\overrightarrow{BC}$的取值范围为[-4,4].