题目内容
13.设a=${∫}_{0}^{π}$$\sqrt{2}$cos(x-$\frac{π}{4}$)dx,则二项式(a$\sqrt{x}$-$\frac{1}{\sqrt{x}}$)4中展开式中含x项的系数是( )| A. | -32 | B. | 32 | C. | -8 | D. | 8 |
分析 先根据定积分的计算求出a的值,再根据二项式定理即可求出答案.
解答 解:a=${∫}_{0}^{π}$$\sqrt{2}$cos(x-$\frac{π}{4}$)dx=$\sqrt{2}$sin(x-$\frac{π}{4}$)|${\;}_{0}^{π}$=$\sqrt{2}$[sin$\frac{3π}{4}$-sin(-$\frac{π}{4}$)]=2,
∴(2$\sqrt{x}$-$\frac{1}{\sqrt{x}}$)4的展开式的通项公式为T=C4k(2$\sqrt{x}$)4-k(-$\frac{1}{\sqrt{x}}$)k=T=C4k(2)4-k(-1)k($\sqrt{x}$)4-2k=C4k(-1)k(2)4-kx2-k,
当2-k=1时,即k=1时,
∴T=-C41(2)4-1x2-1=-32x,
故选:A.
点评 本题考查了定积分的计算和二项式定理,属于中档题.

练习册系列答案
相关题目
18.已知等腰直角三角形的斜边的长为2,将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )
| A. | $\frac{2π}{3}$ | B. | $\frac{4π}{3}$ | C. | 2π???? | D. | 4$\sqrt{2}$π |
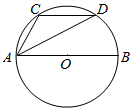 如图,AB是⊙O的直径,点C,D是半圆弧AB的三等分点,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,则$\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$.(用a,b表示)
如图,AB是⊙O的直径,点C,D是半圆弧AB的三等分点,若$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,则$\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$.(用a,b表示)